Лекция: Моделирование многомерных нелинейных систем

Тип 2

быстродействие до 100МГц - АЦП: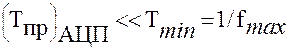

Мультиметры - ,,,.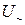

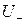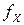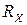В лекции рассматриваются методы решения систем нелинейных уравнений.

Содержание

Решение систем нелинейных уравнений

Метод простых итераций

Решение систем нелинейных уравнений методом Ньютона

Определение матрицы Якоби

В задачах проектирования и исследования поведения реальных объектов, процессов и систем (ОПС) математические модели должны отображать реальные физические нелинейные процессы. При этом эти процессы зависят, как правило, от многих переменных.

В результате математические модели реальных ОПС описываются системами нелинейных уравнений.

Решение систем нелинейных уравнений

Дана система нелинейных уравнений

(10.1)

или

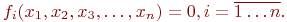
Необходимо решить эту систему, т.е. найти вектор 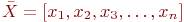, удовлетворяющий системе (10.1) с точностью .

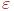Вектор 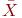определяет точку в n-мерном Евклидовом пространстве, т.е. 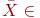этому пространству и удовлетворяет всем уравнениям системы (10.1).

В отличие от систем линейных уравнений для систем нелинейных уравнений неизвестны прямые методы решения. При решении систем нелинейных уравнений используются итерационные методы. Эффективность всех итерационных методов зависит от выбора начального приближения (начальной точки), т.е. вектора

.

Область, в которой начальное приближение 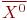сходится к искомому решению, называется областью сходимости G. Если начальное приближение 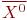лежит за пределами G, то решение системы получить не удается.

Выбор начальной точки во многом определяется интуицией и опытом специалиста.

Дата добавления: 2014-01-14