Метод, основанный на центральной предельной теореме

Этот метод моделирования относится к третьему способу получения последовательности чисел с нормальным законом распределения. Метод основан на приближенном воспроизводстве условий, при которых справедлива центральная предельная теорема теории вероятности.

Согласно центральной предельной теореме, при сложении достаточно большого количества независимых случайных величин с произвольным законом распределения получается случайная величина, распределенная по нормальному закону. Опыт показывает, что при сложении всего шести (k=6) случайных величин равномерно распределенных на интервале [0,1], получается случайная величина, которая с точностью, достаточной для большинства прикладных задач, может считаться нормальной.

Рассмотрим метод аппроксимации нормально распределенной случайной величины Х, основанный на использовании двенадцати (k=12) равномерно распределенных случайных величин.

Алгоритм метода:

1.Сложить 12 равномерно распределенных псевдослучайных чисел yi.

2.Пронормировать полученную сумму, т.е. получить случайную величину T с М(Т)=0 и 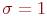, где Т – нормально распределенная случайная величина.

3.Результат привести в соответствие с заданным математическим ожиданием и среднеквадратичным отклонением .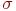

Нормально распределенная случайная величина X с требуемыми значениями математического ожидания и среднеквадратичного отклонения определяется как:

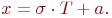
Пусть

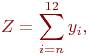
где y_i – независимые равномерно распределенные на интервале [0,1] случайные величины.

Ранее было показано, что математическое ожидание и дисперсия равномерно распределенной на интервале [0,1] случайной величины Y соответственно равны:

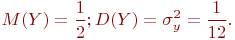
Тогда математическое ожидание суммы Z равно:

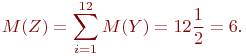
а ее дисперсия D(Z) равна:

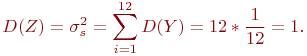
Пронормируем сумму Z, т.е. перейдем от нее к величине:

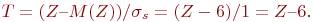
Переходя к требуемым математическому ожиданию a и среднеквадратичному отклонению 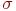, окончательно имеем:

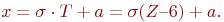
Таким образом, чтобы определить значение нормально распределенной случайной величины с математическим ожиданием, равным нулю, и среднеквадратичным отклонением, равным единице, необходимо взять 12 равномерно распределенных чисел, сложить их, а из суммы вычесть 6, т.е.:

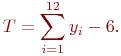(8.4)

Чтобы определить значение нормально распределенной случайной величины с требуемым математическим ожиданием a и требуемым среднеквадратичным отклонением необходимо из суммы двенадцати равномерно распределенных чисел вычесть 6, а результат умножить на и прибавить a, т.е.

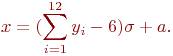(8.5)

Теперь перейдем к генерированию последовательности нормально распределенных случайных чисел.

Рассмотрим датчик нормально распределенных случайных чисел.

Алгоритм датчика (рис. 8.3) реализует метод получения последовательностей псевдослучайных чисел с нормальным законом распределения, основанный на центральной предельной теореме вероятностей. Алгоритм датчика требует обращения к RANDU для вычисления равномерно распределенных случайных чисел.

Назначение датчика GAUSS:

Вычисление нормально распределенного псевдослучайного числа X с заданным математическим ожиданием AM и среднеквадратичным отклонением S.

Обращение к датчику: GAUSS (IX,S,AM,X),

Описание параметров:

IX – параметр необходимый для обращения к RANDU. При первом обращении, IX – целое число с числом цифр 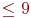. После первого обращения IX=IY, где IY – целое равномерно распределенное случайное число, вычисленное с помощью равномерно распределенных случайных чисел RANDU.

S – требуемое среднеквадратичное отклонение нормального распределения.

AM – требуемое математическое ожидание нормального распределения.

X – значение вычисленной нормально распределенной случайной величины.

Требуемые подпрограммы:

RANDU – датчик равномерно распределенных случайных чисел.

Обращение к RANDU:

RANDU (IX,IY,YF),

где

YF – полученное в результате обращения случайное равномерно распределенное число в интервале [0,1] и представленное в форме с плавающей запятой.

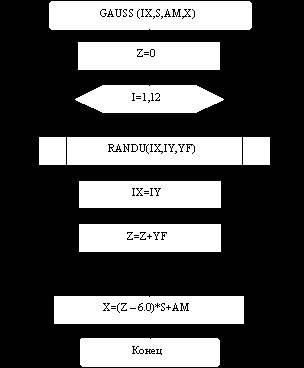
Рис. 8.3. Алгоритм датчика GAUSS

Используя датчик GAUSS, построим алгоритм (рис. 8.4) вычисления последовательности нормально распределенных случайных чисел X с требуемым математическим ожиданием AM и среднеквадратичным отклонением S.

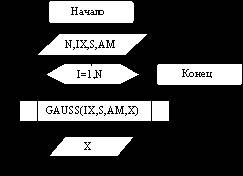
Рис. 8.4. Алгоритм вычисления последовательности нормально распределенных случайных чисел

Исходные данные:

N - длина последовательности нормально распределенных чисел (количество испытаний).

IX - начальное значение, нечетное целое число с числом цифр.

Например.

S, AM – характеристики нормального распределения: среднеквадратичное отклонение и математическое ожидание.

Результат:

X – значение нормального распределения псевдослучайного числа.

Используя различные начальные значения параметра IX, можно формировать различные последовательности нормального распределенных псевдослучайных чисел.

Дата добавления: 2014-01-14