Выбор маршрута прокладки кабеля кольцевой архитектуры

Используемые методы:

1) метод "иди в ближний узел":

- определяем множество узлов, через которое должен пройти кабель кольца;

- определяем расстояние между узлами, формируем матрицу расстояний;

- формируем очередь, элементы которой – расстояния между узлами. В начале очереди – лучи с минимальными расстояниями, а дальше по возрастающей;

- просматриваем всю очередь и формируем маршрут прокладки.

Узлы:

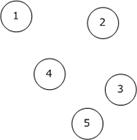
Матрица:

№
	*
		*
			*
				*
					*

Строим очередь: , , , , , , , , ,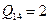

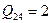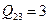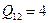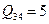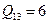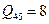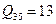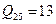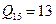
Между любыми двумя узлами должна быть только одна дуга. Получилось:

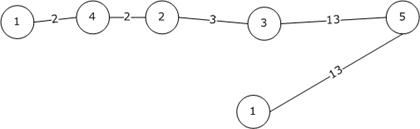
Итого: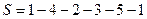, а длина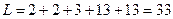

2) метод Прима-Эйлера:

- определяем множество узлов сети;

- определяем расстояния между узлами сети, формируем матрицу расстояний;

- с помощью алгоритма Прима строим остовое дерево;

- стоим мультиграф (каждой дуге в этом дереве сопоставляем идентичную дугу);

- выбираем в полученном мультиграфе маршрут Эйлера (при котором один узел принимаем за базовый, последовательно проходим по всем дугам и удаляем повторно встречающиеся узлы в мультиграфе).

Первые два пункта такие же. Строим остовное дерево:

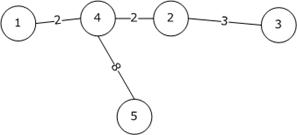
Мультиграф:

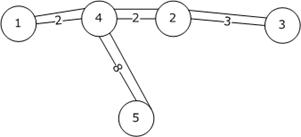
Получилось: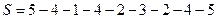

Удаляем повторные узлы: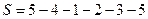

Длина: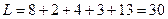

3) метод Литтла:

- найти минимальный элемент в каждой строке и вычесть его из каждого элемента;

- найти минимальный элемент в каждом столбце и вычесть его из каждого элемента;

- для каждого нулевого элемента вычесть сумму минимальных элементов по строке и столбцу;

- выбираем максимальный и исключаем из матрицы расстояний дугу, связывающую его узлы;

исходная:

№
	*
		*
			*
				*
					*

после строки:

№
	*
		*
			*
				*
					*

после столбца:

№
	*
		*
			*
				*
					*

после нулевых:

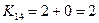
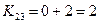
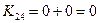
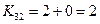
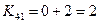
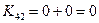
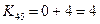- максимальный, исключаем 4 строку и 5 столбец

№
	*
		*
			*
				*

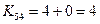
Элемент 54 = *.

И с этой матрицей теперь всё то же самое. В конце получится вот что:

№
	*
		*
			*
				*

Опять для всех нулей находим и выбираем максимальный. Тут будет .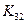

И так далее. В конце останутся дуги (4,5), (3,2), (1,4), (2,1) и (5,3).

Маршрут, например: 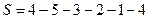и тогда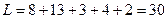

Задание в тетрадь: всеми тремя методами решить и сравнить результаты, рисунок ниже.

№
	*
		*
			*
				*
					*
						*

Потом решить ещё методом "ветвей и границ" и генетическим алгоритмом. Но последние два – это для избранных.

Лекция №7 [20.03.12]

Дата добавления: 2014-01-14