Свойства вероятности как функции события

1. Для каждого события А поля S .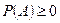

Действительно, т.к. дробь 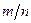не может быть отрицательной.

2. Для достоверного события .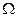

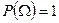Действительно, т.к. достоверному событию благоприятствуют все , .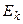

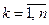3. Если событие А подразделяется на частные случаи В и С и все три события А, В и С принадлежат полю S, то .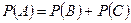

Доказательство. Пусть событию В благоприятствуют 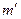, а событию С – 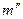событий 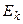системы G. Так как события В и С по допущению несовместны, то события 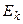, благоприятные одному из них, отличны от событий 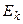, благоприятных другому. Всего, таким образом, имеется 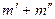событий 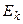, благоприятных появлению одного из событий В или С, т.е. благоприятных событию А=В+С. Следовательно, 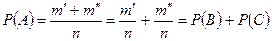. Свойство доказано.

Замечание. Свойство 3 называют теоремой сложения вероятностей несовместных событий. Оно может быть сформулировано так: вероятность наступления хотя бы одного из несовместных событий равна сумме вероятностей этих событий. Свойство 3 можно обобщить на любое конечное число попарно несовместных событий.

4. Вероятность события 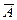, противоположного событию А, равна .

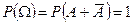Доказательство. Так как , то по свойству 2 . Так как события А и 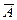несовместны, то по свойству 3 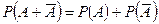. Следовательно, 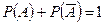и . Свойство доказано.

5. Вероятность невозможного события равна нулю.

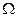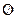Доказательство. События и несовместимы, поэтому , откуда следует, что .

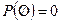6. Если событие А влечёт за собой событие В, то .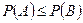

Доказательство. Событие В может быть представлено в виде 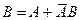. Отсюда в силу свойств 3 и 1 получаем .

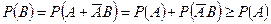7. Вероятность любого события заключена между нулём и единицей.

Доказательство. Из-за того, что для любого события А имеют место соотношения 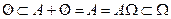, то в силу свойства 7 имеем неравенства: .

Замечание 1. Свойства 2, 5, 7 совпадают со свойствами, полученными из классического определения вероятностей.

Замечание 2. В случае статистического определения вероятности также имеют место свойства 2, 5, 3.

Пример 1. В ящике 30 шаров: 10 красных, 5 синих и 15 белых шаров. Вынули один шар. Найти вероятность появления цветного шара.

Решение. Появление цветного шара означает появление либо красного, либо синего шара. Пусть событие А – появление красного шара, а событие В – появление синего шара. Тогда событие А+В – появление цветного шара. Вероятность события А: 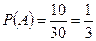. Вероятность события В: 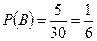. Появление шара одного цвета исключает появление шара другого цвета, поэтому события А и В несовместны. По теореме о сложении вероятностей несовместных событий .

Пример 2. Из колоды в 36 карт наудачу вынимают 3 карты. Найти вероятность того, что среди них окажется хотя бы один туз.

Решение. В рассматриваемой задаче «наудачу» означает, что всевозможные комбинации по 3 карты равновероятны.

1 способ. Пусть событие А – в вынутых 3-х картах окажется хотя бы один туз, т.е. имеет место одно несовместных из событий: либо 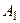- один туз, либо 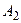- 2 туза, либо - 3 туза. Общее число равновозможных случаев 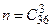. Число случаев, благоприятных событию 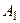равно 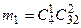, событию 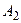– 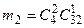, событию – 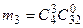. Тогда вероятности событий 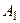, , 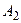равны соответственно

, ,

.

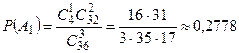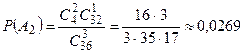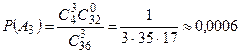В силу теоремы сложения .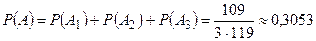

2 способ. Событие 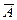, противоположное событию А, состоит в том, что среди вынутых карт не окажется ни одного туза. Три нетуза можно вынуть из колоды карт 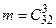способами (число исходов, благоприятных событию 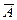). Общее число равновозможных случаев 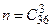. Тогда 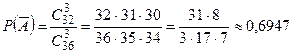, и искомая вероятность равна .

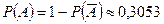Ответ: .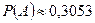

Дата добавления: 2014-01-14