Погрешности измерений

Процедура измерений состоит из следующих основных этапов: принятие модели объекта измерения, выбор метода измерений, выбор средств измерений, проведение эксперимента для получения численного значения результата измерения. Различного рода недостатки, присущие этим этапам, приводят к тому, что результат измерения отличается от истинного значения измеряемой величины.

Классификация погрешностей от причины возникновения погрешностей.

Причины возникновения погрешности могут быть различными. Измерительные преобразования осуществляются с использованием различных физических явлений, на основании которых можно установить соотношение между измеряемой величиной объекта исследования и выходным сигналом средства измерений, по которому оценивается результат измерения. Точно установить это соотношение никогда не удается вследствие недостаточной изученности объекта исследования и неадекватности его принимаемой модели, невозможности точного учета влияния внешних факторов, недостаточной разработанности теории физических явлений, положенных в основу измерения, использования простых, но приближенных аналитических зависимостей вместо более точных, но сложных и т. д. В результате принимаемая зависимость между измеряемой величиной и выходным сигналом средства измерений всегда отличается от реальной, что приводит к погрешности, которую называют методической погрешностью измерения.

В погрешность измерения входит погрешность средств измерений, используемых в эксперименте. Допускаемые значения основной погрешности средств измерений указывают в нормативно-технической документации на эти средства и могут быть указаны на самих средствах. В условиях эксперимента у применяемых средств измерений могут возникнуть дополнительные погрешности из-за влияния внешних факторов (например, температуры окружающей среды, внешнего магнитного поля), неправильной установки прибора (например, вертикальная или наклонная установка прибора, который должен устанавливаться горизонтально).

Следует также иметь в виду, что включение средства измерений в цепь, где производится измерение, может изменить режим цепи за счет взаимодействия средства измерений с цепью (с объектом измерения). Указанные погрешности, обусловленные несовершенством свойств используемых средств измерений, образуют инструментальную составляющую погрешности измерений.

В процессе измерения часто принимает участие экспериментатор. Он может внести субъективную погрешность, которая является следствием индивидуальных свойств человека, обусловленных физиологическими особенностями его организма, скоростью реакции или укоренившимися неправильными навыками. Например, если нескольким экспериментаторам поручить установить одно и тоже значение тока в цепи по аналоговому амперметру, то при всей тщательности установки значения тока будут отличаться друг от друга.

При проведении эксперимента может появиться необходимость в обработке промежуточных результатов измерений. Для этих целей удобно использовать средства вычислительной техники (микрокалькуляторы, микро- или мини-ЭВМ). Они могут внести свою составляющую погрешности, обусловленную неточностью выполнения вычислительных операций.

Таким образом, погрешность измерения образуется из методической погрешности, инструментальной погрешности, погрешности вычислений и погрешности, вносимой оператором.

В зависимости от режима работы (статического или динамического) используемого средства измерений различают погрешности в статическом режиме (статические погрешности) и погрешности в динамическом режиме. В статическом режиме измеряемая величина и выходной сигнал (например, отклонение указателя), по которому оценивают результат измерения, являются неизменными во времени. В динамическом режиме выходной сигнал изменяется во времени. Типичным примером динамического режима работы средства измерений является измерение изменяющейся во времени величины. При измерении постоянной величины динамический режим возникает при подключении средства измерений к исследуемому объекту и продолжается до тех пор, пока выходной сигнал не достигнет постоянного установившегося значения. Особенностью динамического режима является то, что, помимо перечисленных выше погрешностей, характерных для статического режима, здесь возникает погрешность, обусловленная инерционными свойствами средства измерений. Инерция (тепловая, механическая, электрическая) средства измерений приводит к тому, что выходной сигнал не сможет успевать правильно реагировать на быстрые изменения входной измеряемой величины, искажая таким образом представление о характере этих изменений. Погрешность, обусловленную инерционными свойствами, называют динамической погрешностью и определяют ее как разность между погрешностью в динамическом режиме и статической погрешностью, соответствующей значению измеряемой величины в данный момент времени.

В зависимости от способа выражения погрешности измерения различают абсолютную и относительную погрешности. Абсолютную погрешность Dх==х—x₀ выражают в единицах измеряемой величины. Более наглядной характеристикой точности при сравнении различных результатов измерения является относительная погрешность d=Dх/хо. Знак относительной погрешности определяется знаком Dх. Относительная погрешность может быть выражена в процентах.

В зависимости от характера изменения различают:

1) систематическую погрешность измерения—составляющую погрешности измерения, остающуюся постоянной или закономерно изменяющуюся при повторных измерениях одной и той же величины;

2) случайную погрешность измерения — составляющую погрешности измерения, изменяющуюся случайным образом при повторных измерениях одной и той же величины.

Систематические погрешности. Наличие систематических погрешностей может быть обнаружено путем анализа условий проведения эксперимента или повторными измерениями одного итого же значения измеряемой величины разными методами или приборами. Примером постоянной систематической погрешности может быть погрешность, обусловленная несоответствием истинного значения меры, например измерительной катушки сопротивления при косвенном измерении тока, с помощью которой производится измерение, ее номинальному значению.

Примером переменной систематической погрешности может быть погрешность от закономерного изменения напряжения вспомогательного источника питания (разряд аккумулятора), если результат измерения зависит от значения этого напряжения.

Систематические погрешности могут быть в значительной степени исключены или уменьшены устранением источников погрешностей или введением поправок, устанавливаемых на основании предварительного изучения погрешностей мер и приборов, применяемых при измерении, использованием поправочных формул и кривых, выражающих зависимость показаний приборов от внешних условий (например, температуры) и т. д. Систематические погрешности могут быть также исключены путем нескольких проведенных определенным образом измерений (см. § 14-2). Применение того или иного способа зависит от требуемой точности, условий проведения эксперимента, наличия поправочных формул и других причин.

Следует иметь в виду, что полностью исключить систематические погрешности невозможно, так как методы и средства, с помощью которых обнаруживаются и оцениваются систематические погрешности, сами имеют свои погрешности. Поэтому всегда остается неисключенный остаток систематической погрешности.

Случайные погрешности. Эти погрешности, как правило, вызываются сложной совокупностью изменяющихся факторов, обычно неизвестных экспериментатору и трудно поддающихся анализу. Иногда причины, вызывающие случайные погрешности, могут быть известны (например, наводки от внешних электромагнитных полей), но если эти причины сами по себе имеют случайный, хаотический характер, то и погрешности, вызванные ими, будут тоже случайными.

Если причины появления случайных погрешностей известны, то для уменьшения этих погрешностей уменьшают влияние причин на результат измерения (например, экранируют цепи). При невозможности устранения этих причин или когда они неизвестны, влияние случайных погрешностей на результат измерения можно уменьшить путем проведения многократных измерений одного и того же значения измеряемой величины с дальнейшей статистической обработкой полученных результатов методами теории вероятностей.

Иногда к систематическим погрешностям применяют такой же подход, как к случайным. Так, например, неисключенный остаток систематической погрешности рассматривают как случайную величину, которая может иметь любое значение в пределах погрешности средств измерений, с помощью которых выявлялась систематическая погрешность. Аналогично следует поступать в тех случаях, когда систематическая погрешность по тем или иным причинам не может быть исключена в процессе эксперимента. Например, систематическая погрешность от влияния температуры окружающей среды на используемое средство измерений может быть хорошо изучена и составлены таблицы поправок для исключения этой погрешности, но по условиям эксперимента температура не измеряется. В этом случае поправку ввести невозможно, но можно утверждать, что систематическая погрешность имеет некоторое значение в пределах, соответствующих возможному диапазону изменения температуры в процессе эксперимента, т. е. рассматривать эту погрешность как случайную величину.

Кроме перечисленных погрешностей измерения, встречается так называемая грубая погрешность измерения, существенно превышающая ожидаемую погрешность при данных условиях. Результат измерения, содержащий грубую погрешность, иногда называют промахом. Он возникает при внезапных кратковременных изменениях условий эксперимента, например, при кратковременном отключении источника питания, механическом ударе, при неправильном отсчете экспериментатором показаний средств измерений и т. п. Грубые погрешности по своей природе тоже случайны и не могут быть предсказаны заранее. Промахи можно выявить путем обработки методами теории вероятностей результатов повторных измерений одного и того же значения измеряемой величины. После выявления они должны быть исключены.

Результат измерения всегда содержит как систематическую, так и случайную погрешности.

ВЕРОЯТНОСТНЫЙ ПОДХОД К ОПИСАНИЮ ПОГРЕШНОСТЕЙ

Полным описанием случайной величины, а следовательно и погрешности, является ее закон распределения, которым определяется характер появления различных результатов отдельных измерений.

В практике электрических измерений встречаются различные законы распределения.

Нормальный закон распределения (закон Гаусса). Этот закон является одним из наиболее распространенных законов распределения погрешностей. Объясняется это тем, что во многих случаях погрешность измерения образуется под действием большой совокупности различных, независимых друг от друга причин. На основании центральной предельной теоремы теории вероятностей результатом действия этих причин будет погрешность, распределенная по нормальному закону при условии, что ни одна из этих причин не является существенно преобладающей.

Нормальный закон распределения погрешностей описывается формулой

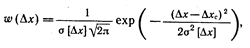
где 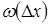— плотность вероятности погрешности 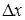; 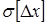— среднее квадратическое отклонение погрешности; 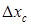— систематическая составляющая погрешности.

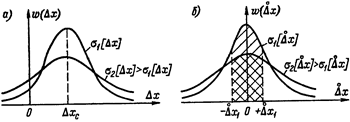
Рис. Нормальный закон распределения погрешности измерений {а) и случайной составляющей погрешности измерений (б)

Таким образом, закон распределения погрешности отличается от закона распределения случайной составляющей погрешности только сдвигом по оси абсцисс на величину систематической составляющей погрешности.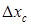

Из теории вероятностей известно, что площадь под кривой плотности вероятности характеризует вероятность появления погрешности. Полная площадь под кривой распределения всегда равна 1, т.е. полной вероятности.

Чем меньше 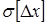, тем реже встречаются большие погрешности, тем точнее выполнены измерения. Таким образом, среднее квадратическое отклонение 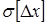можно использовать для характеристики точности измерений:

Равномерный закон распределения. Если погрешность измерений с одинаковой вероятностью может принимать любые значения, не выходящие за некоторые границы, то такая погрешность описывается равномерным законом распределения. При этом плотность вероятности погрешности 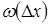постоянна внутри этих границ и равна нулю вне этих границ. Аналитически он может быть записан так:

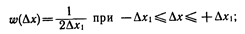
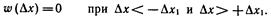
С таким законом распределения хорошо согласуется погрешность от трения в опорах электромеханических приборов, не исключенные остатки систематических погрешностей, погрешность дискретности в цифровых приборах.

Трапециевидный закон распределения. Это распределение графически изображено на рис. а. Погрешность имеет такой закон распределения, если она образуется из двух независимых составляющих, каждая из которых имеет равномерный закон распределения, но ширина интервала равномерных законов различна. Например, при последовательном соединении двух измерительных преобразователей, один из которых имеет погрешность, равномерно распределенную в интервале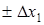, а другой — равномерно распределенную в интервале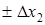, суммарная погрешность преобразования будет описываться трапециевидным законом распределения.

Треугольный закон распределения (закон Симпсона). Это распределение является частным случаем трапециевидного, когда составляющие имеют одинаковые равномерные законы распределения.

Двухмодальные законы распределения. В практике измерений встречаются двухмодальные законы распределения, т. е. законы распределения, имеющие два максимума плотности вероятности. Может быть в приборах, имеющих погрешность от люфта кинематических механизмов или от гистерезиса при перемагничивании деталей прибора.

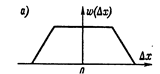
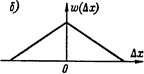
Рис. Трапециевидный (а) и треугольный (б) законы распределения

Если законы распределения погрешностей неизвестны, то они могут быть установлены на основании статистической обработки опытных данных. Однако экспериментальное определение законов распределения весьма трудоемко, поэтому к нему прибегают лишь при весьма ответственных измерениях.

Иногда закон распределения погрешности принимают, исходя из физического представления о причинах появления погрешностей и анализа составляющих погрешностей измерения. Так, например, если погрешность измерения образуется из пяти и более составляющих, среди которых нет существенно преобладающих, то закон распределения результирующей погрешности обычно принимают нормальным. В противном случае, анализируя составляющие погрешности, принимают для них вид законов распределения и методами теории вероятностей находят закон распределения для результирующей (суммарной) погрешности измерения.

Основными числовыми характеристиками законов распределения являются математическое ожидание и дисперсия, которые определяются выражениями:

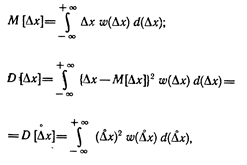
где М — символ математического ожидания; D — символ дисперсии.

Математическое ожидание погрешности измерений есть неслучайная величина, относительно которой рассеиваются другие значения погрешностей при повторных измерениях. Математическое ожидание характеризует систематическую составляющую погрешности измерения. Как числовая характеристика погрешности М показывает на смещенность результатов измерения относительно истинного значения измеряемой величины.

Дисперсия погрешности характеризует степень рассеивания (разброса) отдельных значений погрешности относительно математического ожидания. Рассеивание происходит за счет случайной составляющей погрешность. Чем меньше дисперсия, тем меньше разброс, тем точнее выполнены измерения. Следовательно, дисперсия может служить характеристикой точности проведенных измерений. Однако дисперсия выражается в единицах погрешности в квадрате. Поэтому в качестве числовой характеристики точности измерений используют среднее квадратическое отклонение 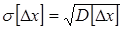с положительным знаком и выражаемое в единицах погрешности.

Максимальные значения погрешности зависят не только от 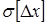, но и от вида закона распределения. Когда распределение погрешности теоретически неограниченно, например при нормальном законе распределения, погрешность может быть любой по значению. В этом случае можно лишь говорить об интервале, за границы которого погрешность не выйдет с некоторой вероятностью. Этот интервал называют доверительным интервалом, характеризующую его вероятность — доверительной вероятностью, а границы этого интервала — доверительными значениями погрешности.

В практике измерений применяют различные значения доверительной вероятности, например: 0,90; 0,95; 0,98; 0,99; 0,9973 и 0,999. Доверительный интервал и доверительную вероятность выбирают в зависимости от конкретных условий измерений.

КЛАССИФИКАЦИЯ СРЕДСТВ ИЗМЕРЕНИЙ

Измерения производят с помощью средств измерений — технических средств, имеющих нормированные метрологические характеристики.

По функциональному назначению средства измерений делят на следующие группы: меры, измерительные преобразователи, измерительные приборы, измерительные информационные системы и измерительные установки.

Под мерой понимают средство измерений, предназначенное для воспроизведения физической величины заданного размера. Например, мерой является резистор, воспроизводящий сопротивление определенного размера с известной погрешностью.

Измерительный преобразователь — средство измерений, предназначенное для выработки сигнала измерительной информации в форме, удобной для передачи, дальнейшего преобразования, обработки и (или) хранения, но не поддающейся непосредственному восприятию наблюдателем. Измерительный преобразователь, к которому подводится измеряемая величина, называют первичным измерительным преобразователем. Измерительный преобразователь, предназначенный для изменения размера величины в заданное число раз, называют масштабным измерительным преобразователем.

В зависимости от рода измеряемой величины на входе измерительные преобразователи для электрических измерений делят на преобразователи электрических величин и преобразователи неэлектрических величин. Примерами преобразователей электрических величин в электрические являются делители напряжения, усилители напряжения и др. Преобразователи неэлектрических величин в электрические применяют при электрических измерениях неэлектрических величин.

Измерительные преобразователи в зависимости от вида (аналоговый, кодированный) входного и выходного сигналов относят к одной из следующих групп: а) аналоговые измерительные преобразователи, у которых на входе и на выходе аналоговые сигналы; б) аналого-цифровые измерительные преобразователи, имеющие на входе аналоговый сигнал, а на выходе кодированный сигнал; в) цифро-аналоговые измерительные преобразователи, у которых на входе кодированный сигнал, а на выходе аналоговый (квантованный) сигнал.

Первичные измерительные преобразователи, размещаемые непосредственно на объекте исследования и удаления от места обработки, отображения и регистрации измерительной информации, называют иногда датчиками.

Измерительным прибором называют средство измерений, предназначенное для выработки сигнала измерительной информации в форме, доступной для непосредственного восприятия наблюдателем, например, в виде цифрового отсчета на отсчетном устройстве. Измерительный прибор, показания которого являются непрерывной функцией изменений измеряемой величины, называют аналоговым измерительным прибором. Например, электроизмерительный прибор с отсчетным устройством в виде стрелки и шкалы — аналоговый прибор.

Измерительный прибор, автоматически вырабатывающий дискретный (кодированный) сигнал измерительной информации и дающий показания в цифровой форме, называют цифровым измерительным прибором.

В зависимости от того, допускают ли измерительные приборы только считывание показаний или допускают считывание и регистрацию или только регистрацию показаний, они относятся либо к показывающим, либо к регистрирующим измерительным приборам. Иногда находят применение так называемые регулирующие измерительные приборы, т. е. приборы, имеющие приспособление для управления технологическим процессом.

Измерительные приборы, которые осуществляют одно или несколько преобразований сигнала измерительной информации в одном направлении в цепи преобразований, называют приборами прямого преобразования. Измерительные приборы, в которых наряду с цепью прямого преобразования имеется цепь обратного преобразования сигнала измерительной информации, называют приборами уравновешивающего преобразования или приборами сравнения, так как в них происходит сравнение измеряемой величины с известной величиной, однородной с измеряемой. В некоторых случаях производится сравнение эффектов, производимых указанными величинами.

В зависимости от применяемых средств (узлов) среди электроизмерительных аналоговых приборов прямого преобразования выделяют следующие группы приборов: электромеханические, электромеханические с преобразователями и электронные.

К группе электромеханических приборов относят электроизмерительные приборы, в которых энергия электромагнитного поля преобразуется в механическую энергию перемещения подвижной части прибора.

К группе электромеханических приборов с преобразователями относят электромеханические приборы с предварительными преобразователями входного сигнала с целью расширения возможностей измерения различных величин.

К группе электронных аналоговых приборов относят приборы, использующие электронные узлы для преобразования сигнала измерительной информации и электромеханический (чаще всего магнитоэлектрический) измерительный механизм.

По роду измеряемой величины электроизмерительные приборы делят наследующие группы: амперметры—для измерения тока; вольтметры — для измерения напряжения; омметры — для измерения сопротивления и т. п.

В зависимости от степени усреднения измеряемой величины выделяют приборы, дающие показания мгновенных значений измеряемой величины, и приборы интегрирующие, показания которых определяются интегралом по времени или по другой независимой переменной от измеряемой величины.

По характеру установки на месте применения приборы бывают стационарными, предназначенными для жесткого крепления, и переносные, не предназначенные для жесткого крепления.

В зависимости от степени защищенности от климатических и механических воздействий приборы выполняют обыкновенными, пыле-, водо-, брызгозащищенными, герметическими, вибро-, удароустойчивыми и др.

Для испытаний крупных объектов, т. е. когда необходимо измерять большое число физических величин, производить обработку измерительной информации, воздействовать на объект в процессе испытаний и т. д., применяют измерительные информационные системы.

Измерительная информационная система — совокупность функционально объединенных измерительных, вычислительных и других вспомогательных технических средств для получения измерительной информации, ее преобразования, обработки с целью представления потребителю (в том числе ввода в АСУ) в требуемом виде либо автоматического осуществления логических функций контроля, диагностирования, идентификации (распознавания образцов).

В последние годы получили применение измерительно-вычислительные комплексы (ИВК), которые представляют собой автоматизированные средства измерений и обработки измерительной информации. Их отличительной чертой является наличие в комплексе свободно программируемой ЭВМ, которая используется не только для обработки результатов измерения, но и для управления самим процессом измерения, а также для управления воздействием (если это необходимо) на объект исследования. ИВК — разновидность ИИС.

Для выполнения массовых технологических измерений применяются измерительные установки. Измерительной установкой называют совокупность функционально и конструктивно объединенных средств измерений и вспомогательных устройств, предназначенных для рациональной организации измерений.

Все средства измерений по выполняемым метрологическим функциям делят на образцовые и рабочие. Образцовые средства измерений предназначены для поверки с их помощью других рабочих средств измерений. Рабочие средства используют для выполнения всех измерений, кроме измерений, связанных с поверкой, т. е. передачей размера единиц величин.

Дата добавления: 2014-01-14