Геометрическая интерпретация задачи (геометрический (или графический) метод решения задачи)

Рассмотрим задачу ЛП в стандартной форме записи:

max(min) f( )=c1x1+c2x2+…+ cnxn,

(2.15)

при ограничениях (условиях):

a11x1+a12x2+…+ a1nxn b1,
a21x1+a22x2+…+ a2nxn b2,	(2.16)
………
am1x1+am2x2+…+ amnxn bm,
xj0, j =	(2.17)

Рассмотрим эту задачу на плоскости, т.е. при п=2. Пусть система неравенств
(2.15)-(2.17) совместна (имеет хотя бы одно решение):

a11x1+a12x2b1,
a21x1+a22x2b2,
………
am1x1+am2x2bm,
x10, x20.

Каждое неравенство этой системы геометрически опреде­ляет полуплоскость с граничной прямой a_i1x₁+a_i2x₂=b_i, i=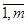. Условия неотрицательности определяют полуплос­кости соответственно с граничными прямыми х₁= 0, х₂= 0. Система совместна, поэтому полуплоскости, как выпуклые множества, пересекаясь, образуют общую часть, которая яв­ляется выпуклым множеством и представляет собой сово­купность точек, координаты каждой из которых составляют решение данной системы. Совокупность этих точек называют многоугольником решений. Это может быть точка, отрезок, луч, замкнутый многоугольник, неограниченная много­угольная область.

Если в системе ограничений (2.15) - (2.17) n = 3, то каж­дое неравенство геометрически представляет полупространство трехмерного пространства, граничная плоскость которого a_i1x₁+a_i2x₂+a_i3x₃=b_i, а условия неотрицательности — по­лупространства с граничными плоскостями соответственно x_j = 0 (j=1,2,3). Если система ограничений совместна, то эти полупространства, как выпуклые множества, пересека­ясь, образуют в трехмерном пространстве общую часть, ко­торая называется многогранником решений.

Пусть в системе (2.15) - (2.17) n > 3, тогда каждое нера­венство определяет полупространство n-мерного пространства с граничной гиперплоскостью a_i1x₁+a_i2x₂+…+a_inx_n=b_i, i=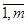, а условия неотрицательности — полупространства с граничными гиперплоскостями x_j = 0, j =.

Если система ограничений совместна, то по аналогии с трехмерным пространством она образует общую часть n-мерного пространства, называемую многогранником реше­ний, так как координаты каждой его точки являются реше­нием.

Таким образом, геометрически ЗЛП (2.15)-(2.17) пред­ставляет собой поиск такой точки многогранника решений, координаты которой доставляют линейной функции наи­большее (наименьшее) значение, причем допустимыми ре­шениями являются все точки многогранника решений.

Если в ЗЛП ограничения заданы в виде неравенств с дву­мя переменными, она может быть решена графически.

ГРА­ФИЧЕСКИЙ МЕТОД РЕШЕНИЯ ЗЛП состоит из следующих этапов.

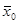Этап 1. Сначала на координатной плоскости x₁ 0 x₂ стро­ится допустимая многоугольная область (область допусти­мых решений, область определения), соответствующая огра­ничениям, которая является пересечением множества полуплоскостей. Далее строится вектор-градиент линейной (целевой) функ­ции f() в какой-нибудь точке , принадлежащей допус­тимой области:

Этап 2. Строится прямая c₁x₁+c₂x₂=f(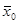) (целевая функция),перпендикулярная век­тору-градиенту, так, чтобы она пересекала допустимую область. Затем прямая передвигается в направлении этого вектора в случае максимизации f() до тех пор, пока не покинет пределов многоугольной области. Предельная точка (или точки) области при этом движении и является точкой мак­симума f().

Этап 3. Для нахождения координат точки максимума достаточно решить два уравнения прямых, получаемых из соответствующих ограничений и дающих в пересечении точку максимума. Значение f(), найденное в получаемой точке, является максимальным.

В случае минимизации f() прямую c₁x₁+c₂x₂=f(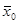) надо двигать в направлении, противоположном вектору-гра­диенту. Ясно, что если прямая при своем движении не по­кидает допустимой области, то соответствующий максимум или минимум f() не существует (целевая функция не ограничена на множестве и задача не имеет оптимальных решений).

▼

Пример. Решить графическим методом следующую ЗЛП:

max f( )=30x₁+60x₂

x₁+3x₂21

3x₁+2x₂21

3x₁+x₂18

x_1,20

Прямые ограничения означают, что область решений будет лежать в первой четверти декартовой системы координат; отметим штриховкой эту область на рис.1.

Этап 1. Определим множество решений первого нера­венства. Оно состоит из решения уравнения и строгого не­равенства. Решением уравнения служат точки прямой
x₁+3x₂-21=0. Построим прямую по двум точкам (0; 7) и (21; 0), которые легко получить в результате последователь­ного обнуления одной из переменных. На рисунке обозначим ее цифрой I.

Множество решений строгого неравенства — одна из по­луплоскостей, на которую делит плоскость построенная пря­мая. Какая из них является искомой, можно выяснить при помощи одной контрольной точки. Если в произвольно взя­той точке, не принадлежащей прямой, неравенство выпол­няется, то оно выполняется и во всех точках той полуплос­кости, которой принадлежит контрольная точка, и не вы­полняется во всех точках другой полуплоскости. В качестве такой точки удобно брать начало координат. Подставим ко­ординаты (0; 0) в неравенство, получим -21<0, т.е. оно вы­полняется. Следовательно, областью решения неравенства служит нижняя полуплоскость.

Аналогичным образом построим области решения двух других неравенств

3x₁+2x₂ -21=0, x₁=0, x₂=10.5,

x₂=0, x₁=7.

(на рисунке прямая II);

3x₁+2x₂ -21 < 0 при x₁= x₂=0, -21<0 выпол­няется, берется нижняя полуплоскость.

3x₁+x₂ -18=0, x₁=0, x₂=18,

x₂=0, x₁=6.

(на рисунке прямая III);

3x₁+x₂ –18 < 0 при x₁= x₂=0, -18 < 0 выполняется, берется нижняя полуплоскость.

Заштрихуем общую область для всех неравенств, обозна­чим вершины многоугольника латинскими буквами и опре­делим их координаты, решая систему уравнений двух пере­секающихся соответствующих прямых. Например, опреде­лим координаты точки С, являющейся точкой пересечения второй и третьей прямой:

3x₁+2x₂ =21, x₂=3, x₁=5

3x₁+x₂ =18.

Вычислим значение целевой функции в этой точке:

f(X)= 30x₁+60x₂ = 150+180=330.

Аналогично поступим для других точек, являющихся вер­шинами замкнутого выпуклого многоугольника OABCD, представляющего собой область допустимых решений рассмат­риваемой ЗЛП. Координаты этих вершин имеют следующие значения: т.О(0;0),
т.А(0;7), т.В(3;6), т.С(5;3), т.Д(6;0).

Этап 2. Приравняем целевую функцию постоянной ве­личине a: 30x₁+60x₂ = а.

Это уравнение является множеством точек, в котором целевая функция принимает значение, равное а. Меняя зна­чение а, получим семейство параллельных прямых, каждая из которых называется линией уровня. Пусть а=0, вычис­лим координаты двух точек, удовлетворяющих соответст­вующему уравнению 30x₁+60x₂ = 0. В качестве одной из этих точек удобно взять точку О(0;0), а так как при x₁=2, x₂=-1, то в качестве второй точки возьмем точку G(2;-1).

Через эти две точки проведем линию уровня f( )=30x₁+60x₂ = 0 (пунктирная прямая на рис.1).

Рис.1

Этап 3. Для определения направления движения к оп­тимуму построим вектор-градиент 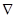, координаты которого являются частными производными функции f( ), т.е. 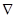=(с₁,с₂) = (30;60). Чтобы построить этот вектор, нужно соединить точку (30;60) с началом координат. При макси­мизации целевой функции необходимо двигаться в направ­лении вектора-градиента, а при минимизации — в противо­положном направлении. Для удобства можно строить век­тор, пропорциональный вектору 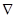. Так, на рис.1 изобра­жен вектор
1/3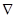= (10;20).

В нашем случае движение линии уровня будем осущест­влять до ее пересечения с точкой В; далее она выходит из области допустимых решений. Следовательно, именно в этой точке достигается максимум целевой функции. Отсюда лег­ко записать решение исходной ЗЛП: max f( )=450 и дости­гается при x₁=3, x₂=6.

Если поставить задачу минимизации функции f( )=30x₁+60x₂ при тех же ограничениях, линию уровня не­обходимо смещать параллельно самой себе в направлении, противоположном вектору-градиенту 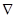. Как это видно на рис.1, минимум целевой функции достигается в точке О(0; 0), следовательно, можно записать min f( )=0 и достигается при, x₁=0, x₂=0.

▲

При решении некоторых ЗЛП графическим методом мо­жет встретиться случай, когда линия уровня параллельна одной из сторон выпуклого многоугольника допустимых решений, причем эта сторона расположена в направлении смещения линии уровня при стремлении целевой функции к своему оптимуму. В этом случае оптимальное значение целевой функции достигается не в одной, а в двух угловых точках (вершинах) многоугольника решений и, следовательно, во всех точках отрезка, соединяющего эти вершины, т. е. задача будет иметь бесчисленное множество решений.

Если область допустимых решений является незамкнутым выпуклым многоугольником в направлении оптимизации целевой функции, то целевая функция будет неограниченной и ЗЛП не будет иметь решений; в этом случае условно можно записать, что, например, max f( )=+∞.

Очевидно также, что ЗЛП не будет иметь решений в случае, когда область допустимых решений есть пустое множество, т. е. система ограничений ЗЛП содержит противоречивые неравенства, и на координатной плоскости нет ни одной точки, удовлетворяющей этим ограничениям.

Дата добавления: 2014-01-14