Выражение (1.2.3) называется рядом Фурье в тригонометрической форме

Или

Тогда

Из математики известно, что

Важнейшим свойством гармонического сигнала является то, что при прохождении через линейные электронные цепи этот сигнал не меняет своей формы, а изменяет только амплитуду и начальную фазу. Это свойство позволяет использовать гармонические колебания при анализе линейных цепей.

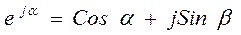. (1.1.3)

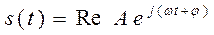(1.1.4)

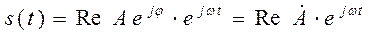, (1.1.5)

где – комплексная амплитуда гармонического колебания.

Комплексной амплитудой гармонического колебания называется такое комплексное число, модуль которого равен действительной амплитуде гармонического колебания, а аргумент – начальной фазе гармонического колебания.

1.2. Спектры периодических сигналов

Рассмотрим произвольный периодический сигнал с периодом Т (рис.1.2).

Из математики известно, что на интервале Т сигнал можно представить в виде набора гармонических колебаний вида (разложение в ряд Фурье):

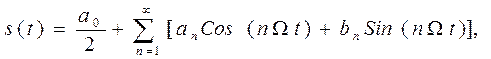(1.2.1)

где ao/2, an, bn – коэффициенты ряда Фурье, которые связаны с сигналом s(t) следующими выражениями:

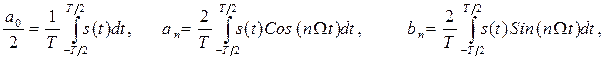(1.2.2)

где Ω = 2π/T – основная частота периодического сигнала или частота первой гармоники сигнала, частоты ωn = nΩ называются частотами высших гармоник сигнала.

Выражение (1.2.1) можно переписать в виде:

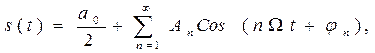(1.2.3)

где 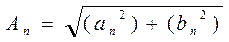- действительная амплитуда n-ой гармоники сигнала, 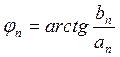- начальная фаза n – ой гармоники сигнала.

Величина ао /2 называется постоянной составляющей сигнала или его средним значением.

Совокупность амплитуд (An) гармонических составляющих сигнала и ао/2 называется амплитудным спектром периодического сигнала или его амплитудно-частотной характеристикой (АЧХ).

Совокупность начальных фаз (φn) гармонических составляющих сигнала называется фазовым спектром периодического сигнала или его фазочастотной характеристикой (ФЧХ).

Совокупность амплитуд (An), (φn), ао /2 и Ω полностью определяют периодический сигнал.

Дата добавления: 2014-01-14