Измерение частоты методом сравнения двух колебаний

Для сравнения частот синусоидальных колебаний можно использовать «метод фигур Лиссажу». В этом случае одно колебание подается на вход «X», а второй - на вход «Y» (см. рис.3.3.). Если соотношение между частотами двух колебаний равно отношению двух простых чисел, то на экране появляется неподвижная фигура, называемая фигурой Лиссажу. По числу пересечений (см.рис.3.4.) фигуры Лиссажу с осями координат можно определить отношение частот двух колебаний, т.к. существует следующая закономерность

(3.2.)

Если известна частота одного колебания, то частота другого может быть определена по выражению

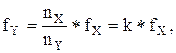(3.3.)

где n_Y,n_X − число пересечений фигуры с осью ОY OX соответственно, f_X − образцовая частота (например, частота сети 50 Гц.).

Примечание: 1.Во избежание потери некоторых точек пересечения не следует проводить секущие фигуру прямые через узловые точки (см. рис.3.3.)

2.Метод фигур Лиссажу применяется при соотношении частот не выше 6÷8 и только для колебаний синусоидальной формы.

Второй метод получил название «метода круговой развертки и модуляции луча по яркости». С помощью двух синусоидальных напряжений U_Y и U_X (рис.3.5,а) сдвинутых по фазе на 90⁰ получают круговую развертку на экране ЭЛТ, а напряжение с неизвестной частотой f_Z подают на модулятор яркости луча − вход «Z».

Известно, что в RC−цепи переменного тока на его элементах возникают падения напряжения

u_R(t) = U_mR*Sinωt, (3.4)

u_C(t) = U_mC*Sin(ωt−π/2) = −U_mC*Cosωt, (3.5)

а отклонение луча по повертикали и горизонтали соответственно равны

L_Y = h_Y* U_mR*Sinωt, (3.6)

L_X = h_X*(−U_mC*Cosωt), (3.7)

где U_mR, U_mC − амплитуды напряжений, подаваемых с RC− фазовращателя на входы осциллографа, h_Y, h_X − чувствительности осциллографа по каналам Y и X.

Если h_Y* U_mR = h_X*U_mC = А, то (3.8)

L_Y² + L_X² = A² (Sin²ωt + Cos²ωt) = A². (3.9)

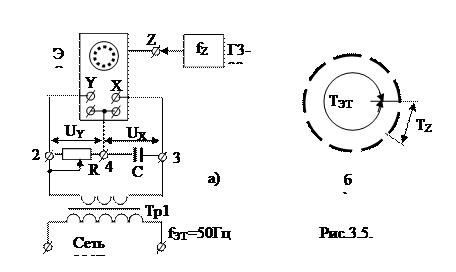Это уравнение окружности, т.е. на экране ЭО появляется изображение окру-жности, модулиро-ванное по яркости напряжением U_z (см.рис.3.5,б).

Подстройкой частоты f_Z добива-ются неподвижного изображения. При этом периоды и частоты эталонного и измеряемого напря-жений находятся в следующих соотношениях:

T_эт = k*T_Z и f_Z = k*f_эт, (3.10)

где k − число яркостных меток на экране ЭО.

Примечание: 1. Точность сравнения очень высокая. Погрешность измерения практически определяется только погрешностью эталонной, образцовой частоты, источником которой может быть выбран перестраиваемый генератор стандартных сигналов с тарированными метрологическими характеристиками.

2.Метод пригоден для измерения частоты знакопеременного напряжения любой формы.

Дата добавления: 2014-01-14