
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Аппарат Жордановых исключений
|
|
|
|
Алгоритмы:
1.Разрешающий элемент заменяется «1».
2.Элементы разрешающего столбца не меняются
3.Элементы разрешающей строчки меняют знак.
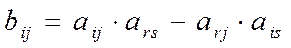 4.Новое значение элемента, которое станет на пересечении столбца и строки
4.Новое значение элемента, которое станет на пересечении столбца и строки
вычисляется по формуле:
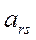
5.Все элементы делятся на значение где:
i-строчка, j-столбец,r-элемент по y (столбцу),s-элемент по x (строке)
 |
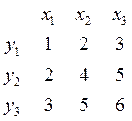
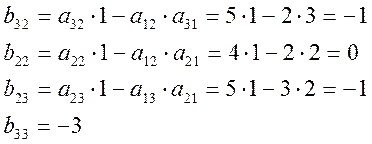
 | |||||||
 | |||||||
 |  | ||||||
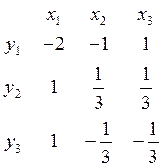
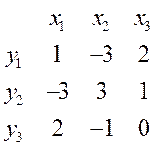
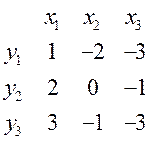




 Ранг матрицы - максимальное число линейно независимых строк, число переброшенных наверх таблицы строк
Ранг матрицы - максимальное число линейно независимых строк, число переброшенных наверх таблицы строк
 | |||
 |
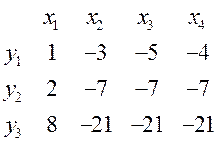


Rang=2( 0 не ЛНЗ)
0 не ЛНЗ)
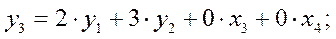
Решение линейных уравнений с помощью шагов Жордановых исключений
2 Метода:
1.Вычеркивание после каждого шага разрешающего столбца
2.Гаусса-вычеркивание после каждого шага и разрешающего столбца и разрешающей строчки.
Алгоритм 1 метода:
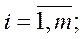
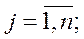
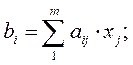 Rang A;
Rang A;
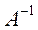
1) Проделав n шагов исключений, получаем обратную матрицу и соответствующее решение 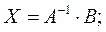
2) Записываем систему уравнений:
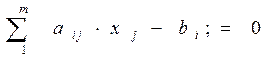
3) Далее эти уравнения переписываются в виде матрицы.
Пример:
решить систему уравнений
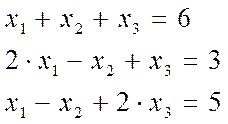
| X2 | X3 | |||
| -6 | ||||
| -1 | -3 | |||
| X3 | |||
| -1 | -1 | ||
| -3 | |||
| X1 | -2 |
| -15 | ||
| X2 | -7 | |
| X1 | -2 |
| X1 | X2 | Xn-1 | Xn | ||
| a11 | a12 | a1n | a1n | b1 | |
| … | … | … | … | … | … |
| am1 | am2 | amn-1 | amn | bm |
| X3 | |
| X2 | |
| X1 |
| X1 | α1 |
| … | … |
| Xn | αn |
↑ разреш. элемент
à
Алгоритм 2 метода:
При вычеркивании столбца и строки необходимо запомнить связь между вычеркиваемыми и переменными
| X3 | |||
| -1 | -1 | ||
à *
à X1=X2-2X3+5 à
| X3 | ||
| -15 | ||
| X3 |
à X2=3X3-7 à à
X3=3; X2=2; X1=1.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 2409; Нарушение авторских прав?; Мы поможем в написании вашей работы!