Основные понятия линейного программирования

Задачи линейного программирования самые простые => самые изученные. Они используются для детерминированных моделей, то есть:

1) эффективность линейно зависит от элементов решения х₁..х_n.

2) ограничения, которые накладываются на элементы решения, имеют вид линейных равенств или неравенств относительно х₁..х_n.

Определение линейного программирования: метод математического программирования, разработанный для оптимизации использования ограниченных ресурсов.

Задачи линейного программирования включают в себя три основных этапа:

1. определение переменных, которые заданы в условиях задачи;

2. определение целевой функции, которую будет оптимизировать;

3. определение ограничений, которым должны удовлетворять переменные.

Пример. Есть сотрудник некой фирмы, которому надо в течение 5 недель 5 раз посетить город Б. Сам он находится в городе А. В первый раз он должен быть в городе Б в понедельник первой недели, последний – в среду пятой недели. Билет из А в Б туда и обратно стоит 400$, но если вылет приходится на конец недели, то на 20% дешевле. Если брать билет в одну сторону, то это будет 75% от стоимости билета. Задача – минимизировать затраты.

Решение (3 этапа)

1. Определить альтернативное решение, которое существует.

2. Определить, какие накладываются ограничения.

3. Выбрать критерий отбора из альтернативных решений.

I. Решение

1. Первое возможное решение – купить пять билетов туда и обратно, но фирма не согласна.

2. Первый билет из А в Б, далее 4 билета туда и обратно на конец недели из А в б и один билет из Б в А на нужную дату.

3. Для первой недели – на понедельник туда и обратно так, чтобы между датами попадала среда, а первый из вылетов приходился на конец недели. Первый и последний билеты покупаются на конец недели. 4 билета тада и обратно: вылеты приходились на конец недели.

II. Ограничения

Дни недели.

III. Критерий отбора

Цена.

1) 5x400$=2000$

2) 2x0,75x400$+4x0,8x400$=1800$

3) 5x(0,8x400$)=1600$

Решением в данном случае является набор переменных, который оптимизирует функцию критерия и удовлетворяет всем условиям.

4.3. Основная задача линейного программирования (ОЗЛП)

как правило, даётся в виде неравенства:

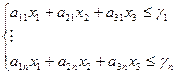
max

h=c₁x₁+c₂x₂+c₃x₃ => оптимизируем целевую функцию

min

x₁..x_n – элементы решения

Пример. Есть сырьё, из которого должно быть изготовлено несколько видов изделия, i=1..3, то есть 3 изделия, а сырья 4. x₁..x₃ – элементы решения, тогда a _ij , где i – вид изделия, а j – вид сырья, - расход сырья на изделие, с₁, с₂, с₃ – прибыль (в

Ограниченияγ₁...γ_n выражаются в наличии на складе сырья (запасов). Задача тогда сводится к след: найти такие неотрицательные значения х₁...х₃, чтобы они удовлетворяли неравенствам с ограничениями γ₁...γ_n, и обращали линейную функцию этих переменных в max or min. Количество изделий не должно быть больше определенного в хз где: х₁≤β₁, x₂≤β ₂, x₃≤β _3.

Общий вид основной задачи линейного программирования:

a₁₁x₁ +... + a_n1x_n = b₁

- - - - - - - - - - (*)

a_1mx₁ +... + a_nmx_n = b_m

α = c₁x₁ +... + с_nx_n => max min (**)

переход от неравенств к равенствам:

дано:

3x₁ + 2x₂ - x₃ ≥ 4

x₁ – 2x₂ + 3x₃ ≤ 10 │×(-1)

α = 4x₁ – x₂ + 2x₃ → max

3x₁ + 2x₂ – x₃ – 4 ≥ 0

-x₁ + 2x₂ – 3x₃ + 10 ≥ 0

Введем новые неотрицательные переменные y₁,y₂

3x₁ + 2x₂ – x₃ = y₁

-x₁ + 2x₂ – 3x₃ =y₂

Найти такие неотрицательные значения x₁…x_n и y₁,y_2, чтобы они удовлетворяли равенствам и обращали целевую функцию в max и min.

Основные критерии, которым должно удовлетворять решение озлп:

1.Допустимость

2.Оптимальность

1.Допсутимое решение - всякая совокупность неотрицательных значений x₁…x_n, удовлетворяющих условию (*)

2. Оптимальное – то из допустимых, которое преобразует функцию (**) в max or min.

Задача может не иметь решений в следующих случаях:

_­1.Уравнения (*) могут быть несовместимыми, т.е. противоречить друг другу

2.Положительных значений решений x₁…x_n может не существовать

3.Решение существует, но оно не оптимально

Дата добавления: 2014-01-14