Последовательный алгоритм компоновки

Будем описывать схему с помощью ГГ: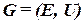

,

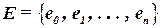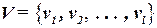
Задача: требуется разбить схему на блоки так, чтобы каждый блок содержал не более чем заданные число элементов 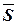и число внешних выводов .

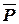В рассматриваемом алгоритме процесс формирования очередного блока начинается с выбора первого, так называемого базового элемента (БЭ). В качестве БЭ выбирается элемент, имеющий максимальное число общих цепей со всеми еще нераспределенными элементами (элемент e₀ уже распределен). далее блок последовательно заполняется элементами из числа еще нераспределенных. Для этого из множества всех нераспределенных элементов выделяется подмножество таких элементов, распределение которых в блок не приводит к превышению заданного числа выводов из блока. Из них в блок распределяется элемент, имеющий максимальное число общих цепей со всеми элементами, уже распределенными в блок. Если таких элементов несколько, то среди них выбирается элемент, при добавлении которого в блок число выводов из блока минимально. Если и таких элементов несколько, то выбирается элемент с максимальным порядковым номером (для формализации задачи).

Рассмотрим более подробно процедуру формирования блока b_j. Будем считать, что блоки b₁, b₂, …, b_j-1 уже сформированы. Пусть I_j – множество элементов, нераспределенных в эти предшествующие блоки, т. е.

,

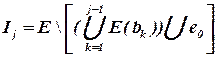где E(b_k) – множество элементов блока b_k.

Последовательный алгоритм компоновки можно представить в следующем виде.

П. 1.

При выборе БЭ для всех элементов вычисляется оценка L₁(x).

,

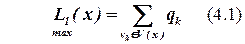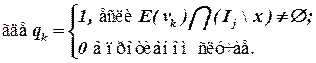
Здесь q_k – связи элемента со всеми нераспределенными элементами,

V(x) – множество цепей, инцидентных элементу x,

E(v_k) – множество элементов, инцидентных цепи v_k,

L₁(x) – число связей элемента x со всеми еще неразмещенными элементами.

В блок распределяется элемент с максимальной оценкой L₁(x). Если таких элементов несколько, то выбирается элемент с большим порядковым номером (для формализации задачи).

П. 2.

Пусть на t -м шаге формирования блока b_j имеется множество элементов 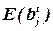, распределенных к этому шагу в блок b_j (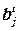). При определении очередного элемента для всех нераспределенных элементов 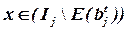вычисляется оценка L₂(x).

,

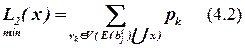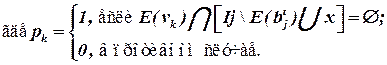
Здесь 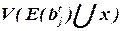– множество цепей, инцидентных всем элементам блока b_j к шагу t, включая элемент x,

L₂(x) – число выводов блока b_j на шаге t с учетом элемента x.

П. 3.

Для всех элементов x, для которых выполняется условие 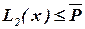, вычисляется оценка L₃(x) – число связей элемента x с формируемым блоком .

,

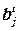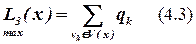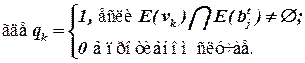
В блок b_j включается элемент с максимальной оценкой L₃(x). Если таких элементов несколько, то среди них выбирается элемент с минимальной оценкой L₂(x). Если и таких элементов несколько, то выбирается элемент с максимальным порядковым номером (для формализации задачи).

П. 4.

Если ни для одного элемента 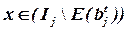условие 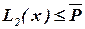не выполняется, то дополнение блока b_j прекращается и начинается формирование следующего блока (переход к п.1).

П. 5.

Алгоритм заканчивает работу когда все элементы схемы распределены в блоки.

При практической реализации алгоритма вместо формулы (4.2) для определения числа выводов из блока удобно использовать формулы для приращения числа выводов из блока b_j при добавлении в него элемента x.

,

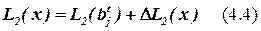где 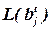– количество выводов блока b_j до добавления в него элемента x.

,

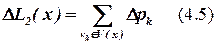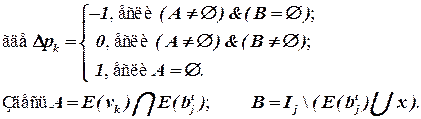
Последнее выражение (для ∆ p_k) можно пояснить с помощью рисунка 4.1.

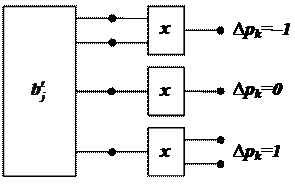
Рис. 4.1.

Рассмотрим работу последовательного алгоритма компоновки на примере.

Пусть необходимо разбить схему, приведенную на рисунке 4.2 на типовые блоки с числом элементов 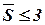и числом выводов 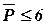, минимизируя при этом количество межблочных связей.

Перед началом компоновки множество нескомпонованных элементов I₁ содержит все элементы схемы кроме e₀ (элемент e₀ уже распределен).

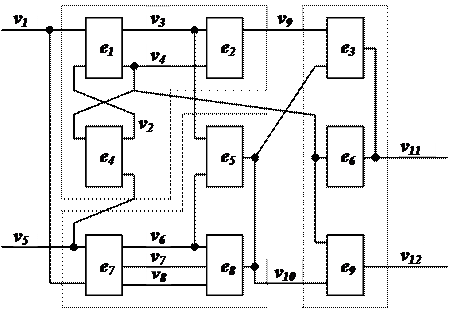
Рис. 4.2.

Для выбора БЭ вычислим оценку L₁(x) по формуле (4.1) для всех элементов множества I₁.

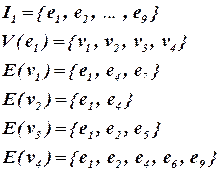
В соответствии с формулой (4.1) .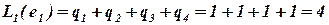

Вычисляя подобным образом оценки L₁(x) для элементов e₂, e₃, …, e₉ определим, что максимальным числом связей со всеми еще неразмещенными элементами обладает элемент e₇ – .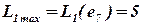

Аналогично вычисляются оценки L₂(x) и L₃(x). Вычислим, например, L₃(e₉) – связи элемента e₉ с элементами формируемого блока, в который вошли элементы e₇ и e₈ (см. ниже).

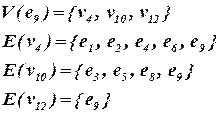
Таким образом .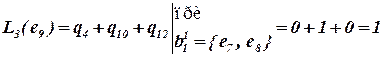

Результаты вычислений удобно свести в таблицу.

	L1	L2	L2	L3	L1	L2	L1	L2	L3
e1		5+3>6	4+3>6	––	4*	––	––	––	––
e2		5+3>6	4+3>6	––		4+1		4+1	2*
e3		5+3>6	4+2=6			4+3	––	4+3	––
e4		5+2>6	4+2=6			4+0	3*	––	––
e5		5+2>6	4+0<6*		––	––	––	––	––
e6		5+2>6	4+2=6			4+1		4+1
e7	5*	––	––	––	––	––	––	––	––
e8		5-1<6*	––	––	––	––	––	––	––
e9		5+3>6	4+2=6			4+2		4+2

В качестве БЭ блока b₁ выбираем элемент e₇ с максимальной оценкой L₁(x)=5.

Для остальных элементов схемы вычисляем оценку L₂(x) – выводы. Результаты сведем в графу 3 таблицы.

Всего один элемент e₈ может быть включен в блок b₁ без нарушения контактного ограничения 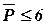. Таким образом, 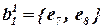, количество выводов из блока – четыре.

Для выбора очередного элемента блока b₁ вычислим оценки L₂(x) для нескомпонованных элементов (графа 4 таблицы).

Для элементов (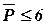) e₃, e₄, e₅, e₆, e₉ вычислим оценки L₃(x) – связи (графа 5таблицы).

При одинаковых максимальных оценках L_3max=2 элемент e₅ дает меньшее число выводов из блока (четыре) чем элемент e₄, поэтому состав блока b₁={e₇, e₈, e₅}; P₁=4, S₁=3.

Формирование второго блока проведем аналогично первому (графы 6 – 10).

Состав b₂={e₁, e₄, e₂}.

Оставшиеся элементы распределим в блок b₃ с P₃=6.

Количество межблочных связей при данном варианте компоновки – десять.

При решении задачи компоновки на ПЭВМ целесообразно использовать списки элементов по цепям и списки цепей по элементам с соответствующими разделителями (см. § 2, Гиперграф).

Для схемы рис. 4.2 список элементов по цепям и соответствующий список разделителей имеют следующий вид:

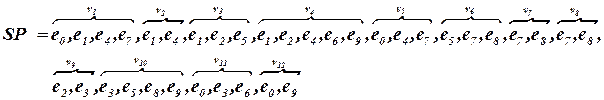
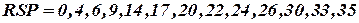
Аналогично составляются список цепей по элементам ST и список разделителей RST.

Схема последовательного алгоритма компоновки приведена на рисунке 4.3.

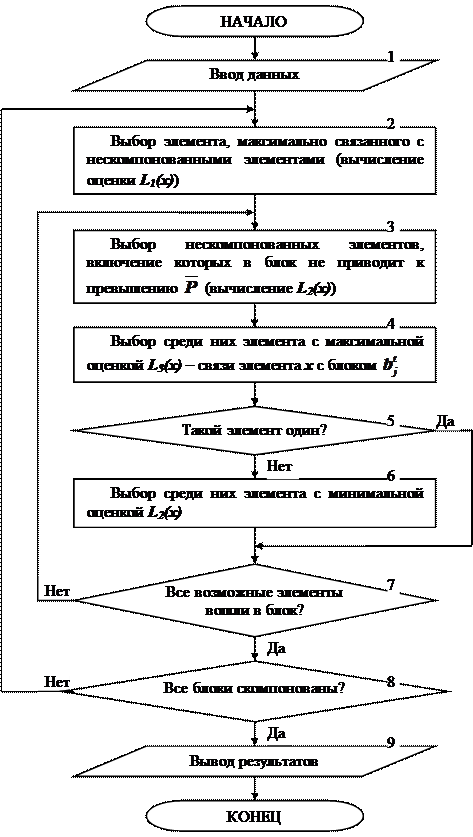
Рис. 4.3. Схема последовательного алгоритма компоновки

§ 5. ЗАДАЧА РАЗМЕЩЕНИЯ КОНСТРУКТИВНЫХ МОДУЛЕЙ

Различают два типа задач размещения:

1) размещение конструктивных элементов в заранее фиксированные позиции;

2) размещение элементов в непрерывном монтажном пространстве, когда позиции заранее не определены, а определяются в процессе размещения (например, проектирование БИС).

Рассмотрим первую задачу.

Пусть имеется регулярное монтажное пространство с уже фиксированными позициями , а также имеется количество 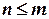элементов для размещения.

Будем считать, что длина связей определяется расстоянием между геометрическими центрами соответствующих позиций, т. е.

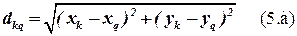
Чаще всего такая метрика используется тогда, когда последующая трассировка соединений осуществляется с помощью проводного монтажа «в навал» (провода с изоляцией). При использовании печатного или жгутового монтажа используются соответственно метрики (5.б) и (5.в):

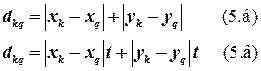
где t – количество проводников в жгуте.

Метрики (5.б) и (5.в) обычно используют тогда, когда наряду с минимизацией суммарной взвешенной длины связей стараются минимизировать также длину наиболее длинной связи (она определяет время задержки схемы).

Если для простоты рассуждений положить m=n, то вариантов размещения будет n!, при этом любой вариант размещения может быть задан перестановкой 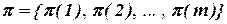, где π(i) – номер позиции, в которую устанавливается элемент e_i.

Сформулируем математическую постановку задачи размещения.

Пусть L(π) – суммарная длина межэлементных соединений, соответствующая некоторому варианту размещения π.

Пусть E_S – множество директивно размещенных элементов, к числу которых, в частности, относятся разъемы и внешние контактные площадки. Здесь S – множество индексов директивно размещенных элементов.

Рассмотрим некоторый произвольный заранее не размещенный элемент. Определим суммарную длину его связей со всеми директивными элементами. Обозначим эту длину как:

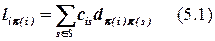
где c_is – элемент матрицы смежности ВНГ.

Суммарная взвешенная длина межсоединений недирективно размещенных элементов e_i и e_j определяется как:

С учетом (5.1) и (5.2) суммарная взвешенная длина межсоединений для варианта размещения π будет определяться из выражения (5.3):

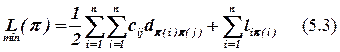
Таким образом, необходимо найти такой вариант размещения 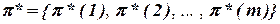при котором обеспечивается минимум целевой функции (5.3). Это комбинаторная задача размещения.

Теперь рассмотрим постановку задачи целочисленного программирования.

Пусть перестановочная матрица (матрица решений) имеет вид:

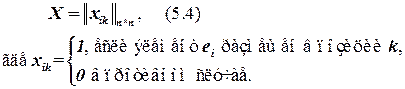
На элементы матрицы решений X можно наложить следующие ограничения:

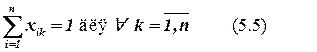Т.е. каждому элементу соответствует одна позиция.

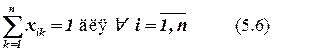Каждый элемент может занимать только одну позицию.

При таком подходе суммарная взвешенная длина межсоединений может быть представлена следующим образом:

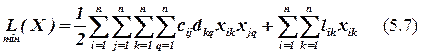
В выражении (5.7) первый член это суммарная взвешенная длина межсоединений между собой недирективно размещенных элементов, второй член – суммарная взвешенная длина межсоединений между недирективно размещенными и директивно размещенными элементами.

Необходимо найти такую булеву матрицу решений X, которая удовлетворяла бы ограничениям (5.4) и (5.6) и обеспечивала минимум целевой функции (5.7). Эта задача является квадратичной задачей целочисленного программирования.

В случае когда элементы не связаны между собой и заранее не фиксированы, а связаны лишь с директивно размещенными элементами, соответствующая задача является задачей линейного назначения. Этот факт используется в ряде приближенных алгоритмов размещения.

В настоящее время разработано много алгоритмов размещения, классификация которых приведена на рисунке 5.1.

Рис. 5.1. Классификация алгоритмов размещения.

Дата добавления: 2014-01-14