
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Итерационные алгоритмы размещения
|
|
|
|
Эти алгоритмы предполагают заданным некоторое начальное размещение, которое может быть получено некоторым конструктивным алгоритмом размещения. Исследуются некоторое множество возможных вариантов размещения близких в некотором смысле к начальному и находящие размещение с меньшим значением целевой функции Lсуммарное. Найденное размещение принимается за исходное и процесс повторяется. Алгоритм заканчивает работу если в окрестности полученного размещения отсутствуют варианты с меньшими значениями целевой функции.
Различают 2 группы итерационных алгоритмов:
- алгоритмы парных перестановок
- алгоритмы групповых перестановок
Алгоритм парных перестановок.
Суть: Последовательное целенаправленное улучшение произвольного начального размещения модулей на плате по выбранному критерию путем парных перестановок. С этой целью на каждой итерации алгоритм осуществляет вычисление приращенной суммарной длины всех связей для всевозможных парных перестановок модулей. Из всего множества перестановок дающих отрицательное приращение выбирается подмножество которое удовлетворяет следующим требованиям:
- выбранное подмножество перестановок позволяет max уменьшить суммарную длину всех связей.
- подмножество образует лишь независимые перестановки в которых модули несвязанны с модулями других переставляющихся пар.
Далее осуществляется перестановки выделенных таким образом пар модулей и переход к следующей итерации.
Описанный итерационный процесс сходится к локальнооптимальному размещению модулей на плате. Выведем формулы для суммарной длины L всех связей и ее приращение  при перемещение модулей.
при перемещение модулей.
Пусть имеется плоское или объемное плато с узлами предназначенными для установки модулей, задана матрица расстояний D=||dij||n*n где dij определяется в обычной или ортогональной метриках.
Даны некоторые совокупности модулей подлежащих размещению и матрица C=||cij||n*m числа связей этих модулей между собой.
Пусть на некоторой итерации имеется следующее размещение модулей на плате:
… 1 2 3 … e … n
 мод t1 t2 t3 … te … tn
мод t1 t2 t3 … te … tn
te- номер модуля оказавшегося размещенным в узле платы.
Поставим в соответствие этому варианту размещения матрицу связей R=||rij||n*n. Элемент rij=числу связей между модулями ti и tj находится на данной итерации в узлах i и j соответственно.
Так как расстояние между узлами i и k равно dik то суммарная длина связей между модулями ti и tk:
lik=rik*dik (1)
отсюда суммарная длина связей ti модуля расположенного в i-ом узле связаны со всеми модульными схемами равна:
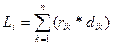 (2)
(2)
Для суммарной длины всех связей при данном варианте получаем формулу:
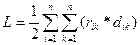 (3)
(3)
Примечание: пусть i=k=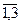 тогда
тогда 
Найдем формулу для приращения суммарной длины всех связей при перестановке мудулей ti и tj расположенных в узлах i и j соответственно.
Для суммарной длины связей ti и tj со всеми остальными модулями имеем:
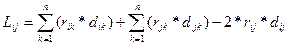 (4)
(4)
Замечание: пусть n=4 i=2 j=3
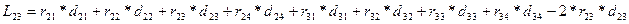
Найдем формулу для приращения суммарной длины всех связей при перестановке модулей ti и tj расположенных в узлах i и j соответственно. Для суммарной длины связей ti и tj модулей со всеми оставшимися модулями имеем:
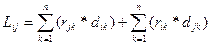 (5)
(5)
Заметим, что за n-ое число перестановок модулей ti и tj соответствует перестановке строк и столбцов с номером i и j в матрице R. Вычитая из (5) выражение (4) определим приращение суммарной длины всех связей после перестановки модулей с номером ti и tj.
 i,j=
i,j=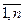 (6)
(6)
Введем в рассмотрение матрицу P=R x D,
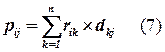 .
.
Полусумма диагональных элементов матрицы P (полуслед) равна суммарной длине всех связей, определяемой формулой (3). С помощью элементов матрицы P могут быть легко вычислены элементы ∆Lij матрицы приращений для всех парных перестановок. С учетом симметричности матрицы D выражение (6) преобразуется к виду:
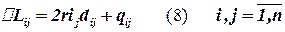 ;
;
где 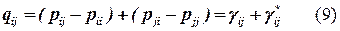
Вычисляя по выражениям (8) и (9) элементы матрицы приращений ∆L можно выбрать подмножество перестановок, удовлетворяющих вышеперечисленным требованиям.
Пример.
Пусть начальное размещение связано с системой модулей на плате с 6-ю узлами имеет вид, представленный на рисунке:
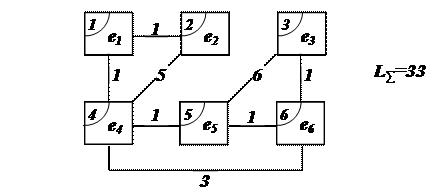
Во втором узле размещен разъем, который запрещено переносить на другую позицию. Если расстояния dij между узлами i и j определены в ортогональной метрике, то матрица D будет иметь вид:
| p1 | p2 | p3 | p4 | p5 | p6 | |||
| p1 | ||||||||
| p2 | ||||||||
| D | = | p3 | ||||||
| p4 | ||||||||
| p5 | ||||||||
| p6 |
| e1 | e2 | e3 | e4 | e5 | e6 | |||
| e1 | ||||||||
| e2 | ||||||||
| R | = | e3 | ||||||
| e4 | ||||||||
| e5 | ||||||||
| e6 |
Составим соответствующую начальному размещению матрицу P=R x D. Элемент p11 определяется из выражения: p11=r11d11+r12d21+r13d31+r14d41+r15d51+ +r16d61= 0+1∙1+0+1∙1+0+0=2 и т. д. и т. п.
| P | = | |||||||
Суммарная длина всех связей в начальном размещении равна полуследу матрицы P: 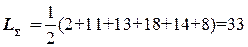 .
.
Вычислим далее последовательно матрицы γ, γ*, Q и ∆L:
| -6 | -3 | -4 | ||||||||
| γ | = | || pij–pii || | = | -5 | -5 | -12 | -7 | |||
| -2 | -10 | -6 | -8 | -4 | ||||||
| -4 | -10 | -6 | ||||||||
| -1 | -4 | -3 |
| -6 | -2 | -1 | ||||||||||
| -5 | -10 | -4 | ||||||||||
| γ* | = | || pij–pii || | = | γT | = | -6 | -10 | |||||
| -3 | -5 | -4 | ||||||||||
| -4 | -12 | -8 | -3 | |||||||||
| -7 | -4 | -6 |
| -6 | -2 | |||||||||
| -20 | -8 | |||||||||
| Q | = | γ+γ* | = | -11 | -22 | -4 | ||||
| симметр. | -2 | -8 | ||||||||
| -9 | ||||||||||
| –– | –– | –– | –– | |||||
| –– | –– | –– | –– | |||||
| ∆L | = | -11 | -2 | |||||
| симметр. | ||||||||
| -7 | ||||||||
∆Lij=2rijdij (>0) +qij (>, <, =0)
В матрице ∆L прочерком указаны элементы, которые заведомо являются положительными в силу положительности соответствующих элементов матрицы Q, а также элементы отвечающие недопустимому переразмещению модуля 2 (разъема). Из рассмотрения матрицы ∆L видно, что к уменьшению суммарной длины всех связей приводят взаимные перестановки пар модулей, расположенных в начальном размещении в следующих узлах: 3 и 4 (∆L =-11), 3 и 6 (∆L =-2), 5 и 6 (∆L =-7).
Примечание. Пары модулей {ei и ej} и {ek и eq} являются независимыми если элементы матрицы связей R равны нулю. Для нашего примера допустимой является лишь одна перестановка (пара 3 и 4), обеспечивающая | ∆Lmax |=11.
Производим перестановку элементов e3 и e4 (см. рис.):
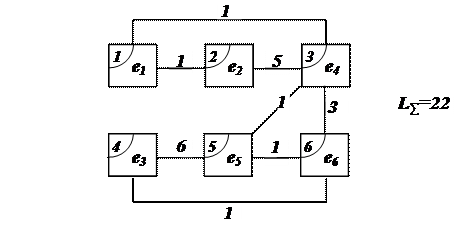
Для нового варианта размещения находим матрицы R и P. С этой целью необходимо в матрице R, соответствующей начальному варианту размещения поменять местами элементы 3-го и 4-го столбцов и 3-ей и 4-ей строк. Матрица P получается умножением новой матрицы R на старую D.
| P | = | |||||||
Суммарная длина всех связей нового варианта
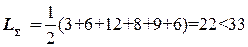 .
.
Выполним следующую итерацию.
| -2 | -2 | |||||||
| -4 | ||||||||
| γ | = | -4 | -2 | |||||
| -7 | ||||||||
| -4 | ||||||||
| -1 |
| -8 | ||||||||
| Q | = | |||||||
| -11 | ||||||||
| –– | –– | –– | –– | –– | ||||
| –– | –– | –– | –– | |||||
| ∆L | = | –– | –– | –– | ||||
| –– | ||||||||
| –– | ||||||||
Матрицы ∆L не имеет ни одного отрицательного элемента, поэтому процесс улучшения начального размещения закончен. Т. о., размещение, изображенное на последнем рисунке соответствует локальному оптимуму.
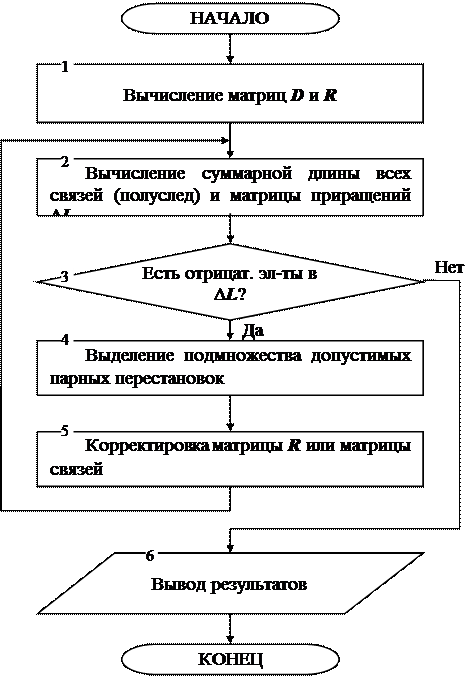
Блок-схема алгоритма парных перестановок.
§ ЗАДАЧА ПОКРЫТИЯ СХЕМ НАБОРОМ КОНСТРУКТИВНЫХ МОДУЛЕЙ.
В результате решения задачи покрытия каждый элемент схемы привязывается к некоторому конструктивному модулю из набора Q={Q1, Q2, …,Qm}.
Математическая постановка задачи покрытия зависит от типа конструктивных модулей набора. Различают 3 типа конструктивных модулей:
1) Каждый модуль содержит базовые логические элементы одного типа, при этом все входы и выходе логических элементов являются выводами модуля.
Например:

2) Тоже что и предыдущий тип, однако в одном конструктивном модуле могут содержаться разнотипные логические элементы.
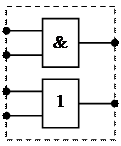
Модули 1-го и 2-го типов называются модулями с несвязанными элементами.
3) Конструктивный модуль в общем случае содержит связанные между собой разнотипные элементы и не все входные и выходные выводы элементов имеются на внешних контактах конструктивного модуля.
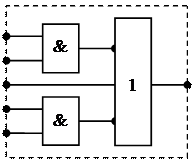
Рассмотрим математическую постановку задачи покрытия схемы конструктивными модулями с несвязанными элементами (1-го и 2-го типов).
Обозначим через bi количество логических элементов ti типа, содержащихся в функционально-логической схеме (ФЛС). При таком подходе состав ФЛС может быть описан матрицей-столбцом: B= || bi || n, где n – число типов логических элементов схемы, bi – число логических элементов ti типа в ФЛС. Будем считать, что каждый тип конструктивного модуля Qj в общем случае содержит несколько типов ti базовых элементов, а весь набор конструктивных модулей Q может быть описан матрицей A= || aij || nxm, где aij – количество базовых логических элементов типа ti в конструктивном модуле типа Qj (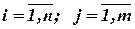 ).
).
Пример.
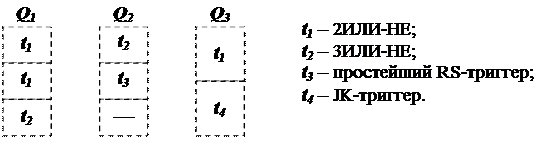
| Q1 | Q2 | Q3 | |||
| t1 | |||||
| A | = | t2 | |||
| t3 | |||||
| t4 |
В качестве критерия оптимизации будем использовать минимум стоимости покрытия. Обозначим cj стоимость конструктивного модуля Qj.
Пусть для покрытия ФЛС необходимо выделить yj конструктивных модулей Qj, тогда в качестве целевой функции можно взять функцию вида:
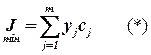 .
.
Будем считать, что каждый тип базового логического элемента схемы может быть реализован как базовый логический элемент того же набора, так и БЛЭ другого типа набора. Например:

Обозначим через xki количество логических элементов типа tk, которое идет на покрытие логических элементов схемы типа ti. Возможность замены БЛЭ типа tk на БЛЭ типа ti будем описывать матрицей W =|| wki || nxn,
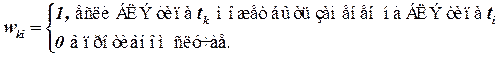
Очевидно, что xki >0 если wki =1.
Учитывая введенные обозначения, задачу покрытия можно сформулировать следующим образом: если yj количество требуемых конструктивных модулей типа Qj, а в каждом Qj конструктивном модуле содержится aij элементов типа ti, то 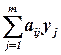 определяет количество логических элементов типа ti, содержащихся во всем выделенном для покрытия ФЛС наборе конструктивных модулей.
определяет количество логических элементов типа ti, содержащихся во всем выделенном для покрытия ФЛС наборе конструктивных модулей.
Очевидно, что для покрытия всей ФЛС необходимо выполнение следующего условия:
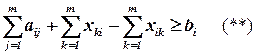 ,
,
где второе слагаемое – количество логических элементов других типов, которые идут в покрытии на реализацию логических элементов типа ti; последнее слагаемое – количество логических элементов типа ti, которые идут на реализацию логических элементов других типов.
Т. о., ставится задача отыскания таких значений yj и xki, удовлетворяющих (**), чтобы обеспечивался минимум целевой функции (*) – стоимости покрытия. На практике используются приближенные методы, опирающиеся на специфику используемых конструктивных модулей. Если имеем дело с несвязанными элементами конструктивного модуля, то здесь в результате определения требуемого числа модулей не осуществляется привязка логических элементов схемы к конструктивным модулям, отсюда появляется возможность оптимизации по другому критерию, в частности по критерию минимума межблочных связей.
Пример Q={Q1, Q2, Q3}, t={t1, t2, t3, t4} приведен нами выше. Требуется покрыть ФЛС, описываемую вектором B={ 5, 4, 1, 1 }, заданным набором конструктивных модулей.
Блок-схема алгоритма определения требуемого числа конструктивных модулей по критерию минимума стоимости покрытия приведена на рисунке.
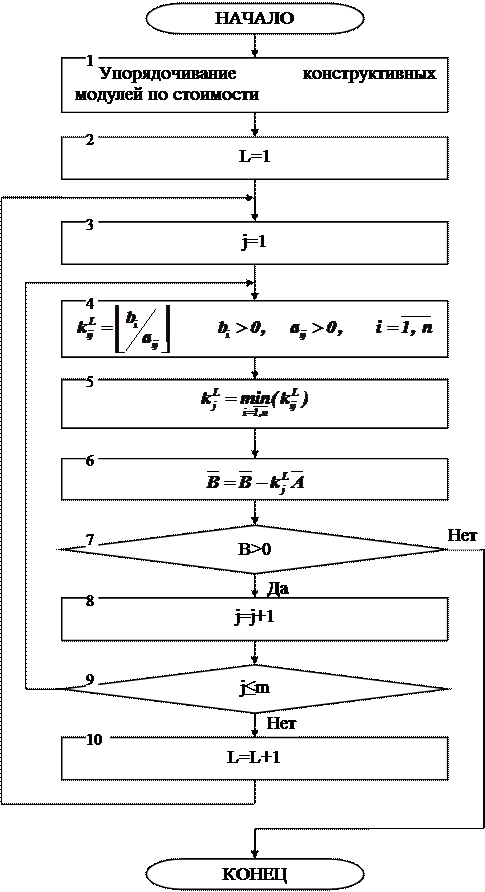
Требуемое число корпусов модуля j-го типа определяется из выражения:
 (1)
(1)
Для нашего примера:
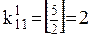

Так как a31=0 и a41=0, то в качестве коэффициента 
Полагаем, что j=2 и вычисляем
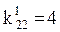 ,
, 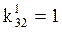 и следовательно
и следовательно 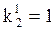
j=3 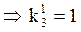
Переходим к 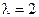 :
:

 , (остальные bi=0)
, (остальные bi=0) 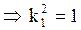
Т.о. имеем 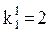 ,
, 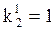 ,
, 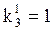 ,
, 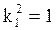 .
.
Эти данные подставляем в выражение (1) и определяем:
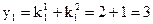 ,
,
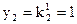 ,
,
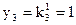 .
.
После определения требуемого числа корпусов, можно осуществить привязку элементов к корпусам. Для этого могут быть использованы рассмотренные ранее алгоритмы решения задач компоновки (задачи разбиения).
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 2926; Нарушение авторских прав?; Мы поможем в написании вашей работы!