Трассировки

ВОЛНОВОЙ АЛГОРИТМ РЕШЕНИЯ ЗАДАЧИ

Большинство алгоритмов конфигурации печатных проводников используют идею волнового алгоритма Ли, который представляет собой процедуру нахождения кратчайшего пути в графе.

В работе Ли плоскость монтажа разбивается на элементарные прямоугольники (ячейки), со стороной равной расстоянию между осями соседних печатных проводников. Минимальная величина прямоугольника (ячейки) определяется технологическим оборудованием.

При использовании ДРП, включение элементарной ячейки в путь означает проведение печатного проводника, так как показано на рисунке 1.

Рис. 1

Считаем, что основная координатная сетка смещена на h/2, чтобы пути следовали из ячейки в ячейку, а не по координатным линиям ДРП.

На каждом шаге алгоритма некоторые ячейки ДРП – заняты. Ячейки, попадающие в область запрещённых для трассировки: краевые поля платы, зоны размещения элементов и их выводы, ранее проведённые проводники.

Основа алгоритма Ли – процедура поиска оптимального, в смысле некоторого критерия, пути между двумя ячейками, при соблюдении ряда условий:

А
	´
		В

· Первая часть алгоритма моделирует процесс распространения волны от элементарной площадки А по свободным ячейкам ДРП. При распространение волны от А, алгоритм последовательно строит Ф₁(А), Ф₂(А), …, Ф_k(А) её фронты. Множество ячеек входящих в i-е фронты для всех i≤k – это окрестность ячейки А. О_k(А).

Если проведение пути возможно, то на k+1 шаге окажется, что ВÎО_k+1(А), если в следующий фронт не удаётся включить ни одной свободной ячейки, т.е.

О_k(А)= О_k+1(А), то при данных условиях путь провести невозможно.

Т.о. первая часть алгоритма Ли определяет возможность проведения пути между А и В.

· Во второй части алгоритма Ли, начиная с В по определённым правилам выполняем переход от ячейки k -го фронта к ячейки k -1 фронта, до тех пор, пока не будет достигнута А. Пройденные ячейки – искомый путь.

Условия, которые д.б. выполнены при проведении пути и возможность оценки его оптимальности д.б. заложены в правила, по которым происходит движение фронта.

Для ячеек ДРП устанавливается отношения соседства (общее ребро). Распространение волны заключается в присваивании соседним ячейкам значения весовой функции. Вес ячейки k -го фронта P_k является функцией веса ячейки k-1 фронта. В общем случае к весам ячеек предъявляются следующие требования: P_k-1¹ P_k ¹ P_k+1, в большинстве модификаций алгоритма Ли на веса ячеек накладывается ограничение: P_k> P_k-1. В этом случае проведение пути заключается в переходе от А к В, т.о. чтобы P_k монотонно убывало. При этом возможен вариант, когда несколько ячеек соседних с данной имеют одинаковый вес. Для однозначного выбора при учёте критерия минимального кол-ва изгибов проводника следует сохранить направление движения. Если приходится делать поворот, то учитываем заранее заданный порядок предпочтений.

Например, пусть P_k= P_k-1+1 – т.е. равно расстоянию k -й ячейки от исходной ячейки А в ортогональной метрике (с учётом запрещённых ячеек). Работа алгоритма для этого случая приведена на рисунке:

												#
			1	2	3	4	5					#
			A			#	6					#
			1			#	7					#
			2			#	8			#	#	#
			3			#	9	10	11	B
			4	5	6	7	8	9	10	11

Рис. 2.

Волна распространяется из А, P_A =0 фронт волны доходит до В на 12 шаге. В ходе построения пути из ячейки (6,9) с Р=11, можно перейти в 3 соседние ячейки с Р=10. здесь переход осуществляется сохраняя направление влево – вверх, аналогично из ячейки с Р=10, у ячейки Р=9, 2 соседних ячейки Р=8, т.к. в этом случае приходится изменять направление движения, то переходим по предпочтённому направлению – вверх. Т.к. вес k -й ячейки в данном варианте равен расстоянию от А, то найденный путь – оптимальный, в смысле его длины. Т.к. алгоритм Ли представляет собой алгоритм нахождения кратчайшего пути в графе, то он легко распространяется на многослойный печатный монтаж, при использовании модификации в виде графа. При наличии ограничения на переходы со слоя в слой можно увеличить вес ребра, соединяющего две смежные вершины графа на соседних слоях, по сравнению с весом ребра графа соединяющего вершины в одном слое. В общем случае весовая функция может зависить от параметров учитывающих длину пути, числа переходов из слоя в слой, степень близости пути к другому и т.д. Например, в виде аддитивной функции:

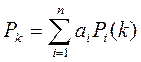
а_i – весовой коэффициент, учитывающий важность i-го параметра.

P_i(k) – значение учитываемого параметра.

Усложнение функции веса увеличивает объём информации на одну ячейку ДРП и время работы 1-й части алгоритма. При практической реализации алгоритма Ли важная проблема – сокращение объёма памяти необходимого для запоминания весов ячеек. При вычислении весов ячеек по выражению: P_k=P_k-1+1 ячейка м.б. в следующих состояниях: свободна, занята или имеет вес от 1 до L (максимально возможная длина пути, определяемое как кол-во ячеек ДРП в пути).

Необходимое, для запоминания состояния одной ячейки, число 2-х разрядов памяти:

«Замечание: перед логарифмом стоит символ = зеркальное отражение Г»

Наиболее эффективным способом кодирования состояния ячеек ДРП является: метод путевых координат по модулю 3. При выборе последовательности, ячеек на этапе построения пути по методу путевых координат, для каждой ячейки, начиная с В (в случае соседства по рёбрам), достаточно знать от какой соседней ячейки в неё пришла волна: ¯(3), ®(2), ­(1), ¬(4). Т.о. ячейка здесь может иметь следующие признаки: свободна, занята, одна из путевых координат, следовательно, число разрядов для кодирования состояния ячеек равно 3.

Путевой координатой C_i фронта Ф_k является та соседняя с ней ячейка C_j фронта Ф_k-1, от которой C_i получила свой вес.

При использовании метода путевых координат соседним ячейкам присваиваются веса в соответствии с пожеланиями пользователя. При проведении пути следует двигаться направлении противоположном распространению волны, в соответствии с путевыми координатами.

Кодирование весов ячеек по mod3.

Оно базируется на том, что P_k-1¹ P_k ¹ P_k+1. Ячейкам включённым в последующие фронты можно присваивать не сами веса, а их значения по mod3 (1,2,3,1,2,3…). Кол-во разрядов на кодирование состояний ячеек равно 3. На практике используется понятие вертикальной и горизонтальной полузанятости ячейки, эти состояния также нужно кодировать.

Проведение пути заключается в отслеживание отметок (1,2,3). Если ячейка имеет несколько соседних ячеек с одинаковыми метками, то используется правило приоритетных направлений.

При движении от ячейки В на рис. 3 используется следующие правило приоритетов:¬, ­, ®, ¯.

												#
				1	2	3	1	2	3			#
				А			#		1			#
							#		2			#
							#		3	#	#	#
							#		1	B

Рис. 3.

Дата добавления: 2014-01-14