Понятие о случайной величине

Основные свойства функций распределения

Понятие случайной величины – основное в теории вероятностей.

Замечание 1. Под случайной величиной понимают некоторую переменную величину, которая в результате испытания под воздействием случайных обстоятельств принимает одно из возможных своих значений, но какое именно – заранее неизвестно.

Примеры. 1. Число очков на грани игральной кости. Множество возможных значений {1, 2, 3, 4, 5, 6}. Вероятность каждого исхода 1/6.

2. Число вызовов, поступивших от абонентов на АТС в течение определённого промежутка времени.

3. Значение скорости молекулы газа в каждый момент времени (случайно зависит от столкновений с другими молекулами).

Замечание 2. Чтобы знать случайную величину, нужно знать:

1) все возможные значения, которые она может принять;

2) как часто (с какой вероятностью) она принимает эти значения.

Определение 1. Если каждому элементарному событию 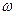из некоторого множества 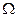можно поставить в соответствие определённую величину 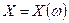– вероятность наступления события 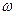, то говорят, что задана случайная величина .

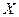Определение 2. Множество 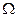называют множеством значений случайной величины.

Замечание 3. Множество 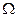может быть конечным, счётным или несчётным, значения могут располагаться дискретно, заполнять сплошь интервалы или не заполнять интервалы сплошь, но располагаться всюду плотно.

Определение 3. Если значения, которые может принимать данная случайная величина Х, образуют дискретный (конечный или счётный) ряд чисел 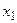, , 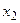…, , …, 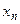то случайная величина Х называется дискретной.

Определение 4. Если значения, которые может принимать данная случайная величина 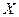, заполняют сплошь некоторый конечный или бесконечный интервал 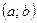, то случайная величина 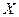называется непрерывной.

Определение 5. Соотношение, устанавливающее связь между возможными значениями случайной величины и их вероятностями, называется законом распределения вероятностей случайной величины.

Замечание 4. Для того, чтобы разнообразные случайные величины с различным характером множества 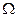и различными законами распределения вероятностей задавать одним и тем же способом, в теории вероятностей вводят понятие функции распределения случайной величины.

Определение 6. Пусть 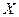– случайная величина, 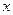– произвольное действительное число. Функция 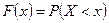(вероятность того, что 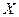примет значение, меньшее 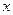) называется функцией распределения вероятности случайной величины Х.

Обозначения: случайные величины 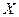, , 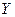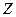; их значения , , .

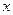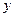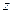Вывод. Случайной величиной называют величину, значения которой зависят от случайных обстоятельств и для которой определена функция распределения вероятностей.

Определение 7 (формальное). Пусть дано множество элементарных событий 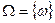. Каждому элементарному событию 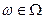поставим в соответствие некоторое число 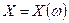. Величина 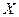называется случайной величиной, если функция 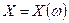измерима относительно введённой на множестве 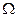вероятности.

Дата добавления: 2014-01-14