Математическое ожидание функции одного случайного аргумента. Пусть задана функция случайного аргумента Х

Пусть задана функция случайного аргумента Х.

Теорема 1. Если Х – дискретная случайная величина, заданная рядом распределения

				…
				…

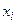
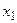
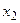
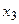
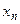
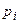
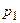
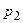
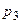
Тогда .

Доказательство. Если дискретная случайная величина Х задана указанным рядом распределения, то случайная величина будет также дискретной с возможными значениями 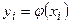(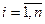). Так как событие «Величина Х приняла значение 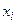» влечёт за собой событие «величина У приняла значение 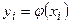», то вероятности возможных значений случайной величины У соответственно равны , , …, :

				…
				…

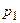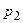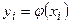
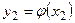
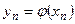
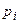
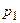
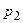
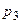
Следовательно, математическое ожидание функции вычисляется по формуле: .

Теорема 2. Пусть непрерывная случайная величина Х заданна плотностью распределения 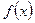. Если 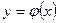дифференцируемая строго монотонная функция, обратная к которой , то математическое ожидание случайной величины У определяется по формуле , где 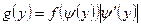– плотность распределения случайной величины У.

Упражнение: доказать.

Теорема 3. Если непрерывная случайная величина Х заданна плотностью распределения 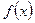, то математическое ожидание функции определяется по формуле .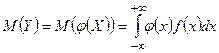

Доказательство. Проводится аналогично доказательству теоремы 1, если вероятность 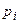заменить элементом вероятности и рассмотреть предел интегральных сумм плотности распределения .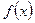

17.3. Функция надёжности

Определение 1. Элементом будем называть любое работающее устройство вне зависимости от его конструкции.

Пусть элемент начинает работать в момент времени 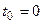, а по истечении времени длительностью 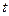происходит отказ. Обозначим Т – непрерывную случайную величину – длительность безотказной работы элемента. Если элемент проработал безотказно (до наступления отказа) время, меньшее, чем 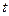, то, следовательно, за время длительностью 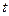наступит отказ. Таким образом, интегральная функция распределения определяет вероятность отказа элемента за время длительностью 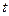. Следовательно, вероятность безотказной работы за это же время длительностью 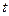, т.е. вероятность противоположного события 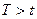равна .

Определение 2. Функцией надёжности называют функцию, определяющую вероятность безотказной работы элемента за время длительностью : .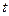

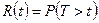Замечание. В некоторых моделях принято считать, что длительность времени безотказной работы элемента имеет показательное распределение с интегральной функцией распределения:

.

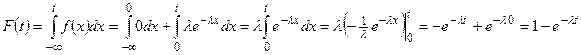Тогда функция надёжности для показательного распределения времени безотказной работы элемента имеет вид: .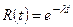

Определение 3. Показательным законом надёжности называют функцию надёжности, определяемую равенством .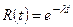

Замечание. Формула 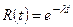позволяет найти вероятность безотказной работы элемента на интервале времени длительностью 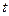, если время работы имеет показательное распределение.

Определение 4. Потоком событий называется последовательность однородных событий, следующих один за другим через какие-либо, вообще говоря, случайные интервалы времени.

Определение 5. Поток событий называется простейшим или пуассоновским (потоком Пуассона, стационарным потоком Пуассона), если в нём число событий, происходящих в течение любого фиксированного интервала времени, имеет распределение Пуассона, и ч и сла событий, происходящих в непересекающиеся промежутки времени, независимы.

Замечание. Если отказы элементов в случайные моменты времени образуют простейший поток, то вероятность того, что за время длительностью 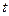не наступит ни одного отказа 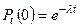. Параметр 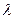характеризует среднюю интенсивность отказов.

Характеристическое свойство. Вероятность безотказной работы элемента на интервале времени 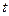не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени 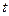(при заданной интенсивности отказов ).

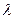Доказательство. Пусть событие А – безотказная работа элемента на интервале времени длительностью ; В – безотказная работа элемента на интервале длительностью 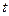. Тогда событие АВ – безотказная работа элемента на интервале длительностью . Тогда вероятности этих событий вычисляются по формуле : , , 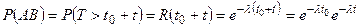. Найдём условную вероятность того, что элемент будет работать безотказно на интервале при условии, что он уже проработал безотказно на предшествующем интервале :

.

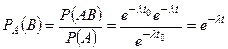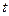Полученная формула не содержит , а содержит только . Это означает, что время работы на предшествующем интервале не сказывается на величине вероятности безотказности работы на последующем интервале, а зависит только от длины последующего интервала, что и требовалось доказать.

Замечание 1. Сравнивая вероятности и 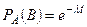, можно сделать вывод, что условная вероятность безотказной работы элемента на интервале длительностью 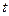, вычисленная в предположении, что элемент проработал безотказно на предшествующем интервале, равна безусловной вероятности этого события. Т.е. безотказная работа элемента «в прошлом» не сказывается на величине вероятности его безотказной работы «в будущем». Это свойство называют марковским свойством или свойством отсутствия последействия.

Замечание 2. Можно доказать, что рассматриваемым свойством обладает только показательное распределение. Поэтому, если при изучении некоторой неизвестной случайной величины получилось, что она обладает этим свойством, то можно сделать вывод, что эта случайная величина распределена по показательному закону.

Дата добавления: 2014-01-14