
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Решение
|
|
|
|
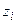
| 1+3=4 | 1+4=5 | 2+3=5 | 2+4=6 | 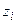
| ||||
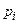
| 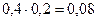
| 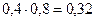
| 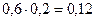
| 
| 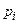
| 0,08 | 0,44 | 0,48 | |
| Сложить вероятности для одинаковых значений Z | Окончательное распределение |
Правило 2. Пусть Х и У – непрерывные независимые случайные величины. Доказано, что закон (плотность) распределения функции 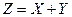 при условии, что дифференциальная функция хотя бы одного из аргументов задана на интервале
при условии, что дифференциальная функция хотя бы одного из аргументов задана на интервале 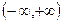 одной формулой, может быть найдена по одному из равенств:
одной формулой, может быть найдена по одному из равенств:
 или
или 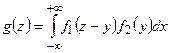 ,
,
где 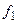 и
и 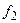 – дифференциальные функции аргументов.
– дифференциальные функции аргументов.
Замечание 1. Если возможные значения аргументов неотрицательны, то закон распределения функции 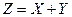 находят по одной из формул:
находят по одной из формул:
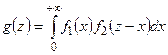 или
или 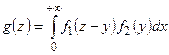 .
.
Замечание 2. Правила можно распространить на любое конечное число независимых случайных величин.
Пример 2. Плотности распределения вероятностей случайных величин Х и У равны  Найти закон распределения функции
Найти закон распределения функции 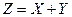 .
.
Решение. По правилу 2 имеем:
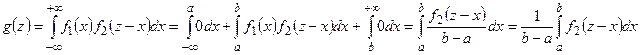 .
.
Надо получить функцию  и пределы её изменения. Так как при
и пределы её изменения. Так как при  выполняется неравенство
выполняется неравенство 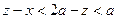 , а при
, а при  – неравенство
– неравенство 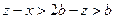 , то при
, то при  и при
и при 
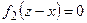 . Пусть
. Пусть 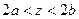 . Функция
. Функция  отлична от нуля только при тех значениях
отлична от нуля только при тех значениях 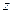 , которые удовлетворяют неравенствам
, которые удовлетворяют неравенствам 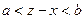 или
или  . Так как
. Так как 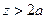 , то
, то 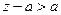 . Очевидно, что
. Очевидно, что 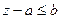 при
при 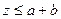 . Следовательно, если
. Следовательно, если 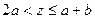 , то
, то 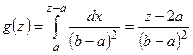 . Аналогично, при
. Аналогично, при 
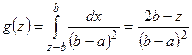 . Тогда
. Тогда
 закон распределения Симпсона.
закон распределения Симпсона.
Определение 2. Дифференциальную функцию суммы независимых случайных величин называют композицией.
Определение 3. Закон распределения вероятностей называется устойчивым, если композиция таких законов есть тот же закон распределения, возможно, что с другими параметрами.
Пример 3. Доказать, что сумма нормально распределённых случайных величин распределена по нормальному закону. Найти математическое ожидание и дисперсию полученного закона распределения.
Замечание 1. В силу примера 3 нормальный закон распределения обладает свойством устойчивости.
Замечание 2. Для независимых случайных величин справедливо и обратное утверждение (теорема Г. Крамера): если сумма двух независимых случайных величин распределена по нормальному закону, то каждое слагаемое также распределено по нормальному закону.
18.2. Законы распределения, являющиеся функциями нормально распределённых независимых случайных величин
18.2.1. Распределение 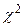
Пусть  (
(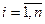 ) – нормальные независимые случайные величины, причём математическое ожидание каждой равно нулю, а
) – нормальные независимые случайные величины, причём математическое ожидание каждой равно нулю, а  .
.
Определение 1. Случайная величина  называется распределённой по закону
называется распределённой по закону 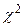 с
с 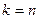 степенями свободы.
степенями свободы.
Определение 2. если указанные случайные величины связаны одним линейным соотношением, то – распределённой по закону 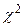 с числом степеней свободы
с числом степеней свободы 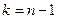 .
.
Дифференциальная функция распределения 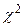 имеет вид:
имеет вид:
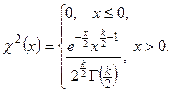 , где
, где 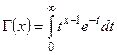 – гамма-функция,
– гамма-функция,  .
.
Распределение 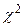 определяется одним параметром – числом степенней свободы
определяется одним параметром – числом степенней свободы 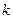 . С увеличением числа степеней свободы распределение медленно приближается к нормальному.
. С увеличением числа степеней свободы распределение медленно приближается к нормальному.
С распределением 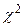 тесно связаны другие распределения:
тесно связаны другие распределения:
| Величина | Плотность распределения при 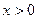
|
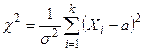
| 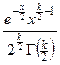
|
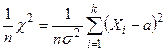
| 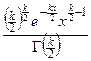
|

| 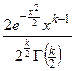
|
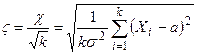
| 
|
При 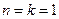  - случайная величина, имеющая плотность распределения, равную удвоенной плотности исходного нормального распределения - случайная величина, имеющая плотность распределения, равную удвоенной плотности исходного нормального распределения
| 
|
При 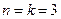 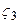 - распределение Максвелла - распределение Максвелла
| 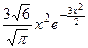
|
18.2.2. Распределение  Стьюдента (псевдоним статистика В. Госсета)
Стьюдента (псевдоним статистика В. Госсета)
Пусть Z – нормальная случайная величина, причём  ,
, 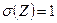 , а V - независимая от Z случайная величина, распределённая по закону
, а V - независимая от Z случайная величина, распределённая по закону  с
с 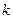 степенями свободы. Тогда величина
степенями свободы. Тогда величина 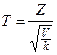 имеет распределение, которое называют
имеет распределение, которое называют  -распределением, или распределением Стьюдента с
-распределением, или распределением Стьюдента с 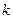 степенями свободы. Плотность распределения задаётся формулой:
степенями свободы. Плотность распределения задаётся формулой: 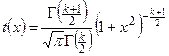 . Значения плотности распределения содержатся в специальных таблицах (значения
. Значения плотности распределения содержатся в специальных таблицах (значения  -распределения).
-распределения).
При малом числе степеней свободы  -распределение далеко от нормального. Однако, с увеличением
-распределение далеко от нормального. Однако, с увеличением 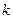 (
( )
) -распределение быстро приближается к нормальному распределению.
-распределение быстро приближается к нормальному распределению.
Доказательство: [5, C.143 – 146].
При 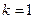
 –распределение Коши.
–распределение Коши.
18.2.2. Распределение  Фишера-Снедекора
Фишера-Снедекора
Если U и Vнезависимые случайные величины, распределённые по закону  со степенями свободы
со степенями свободы 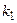 и
и 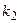 , то величина
, то величина 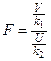 имеет распределение, которое называют распределением
имеет распределение, которое называют распределением  Фишера-Снедекора со степенями свободы
Фишера-Снедекора со степенями свободы 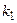 и
и 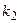 (иногда его обозначают
(иногда его обозначают 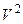 ). Дифференциальная функция распределения
). Дифференциальная функция распределения  имеет вид:
имеет вид:
 где
где 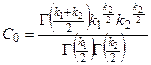 .
.
Распределение  определяется двумя параметрами – числами степеней свободы.
определяется двумя параметрами – числами степеней свободы.
Глава 4. Многомерные случайные величины
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 384; Нарушение авторских прав?; Мы поможем в написании вашей работы!