Второе уравнение Максвела

Второе уравнение Максвела -есть обобщение закона Фарадея на диэлектрические среды.

Закон Фарадея имеет вид:

U=-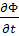; (1.6)

т.е. изменение магнитного потока индукции Ф, пронизывающем проводящий контур создает в этом контуре ЭДС-U.

Максвел утверждал, что переменный магнитный поток создает ЭДС не только в проводящем контуре, но и в замкнутой диэлектрической трубке.

U=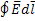; (1.7)

Ф=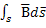; (1.8)

подставляя 1.7 и 1.8 в 1.6 получим

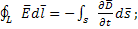(1.9)

-2-е уравнение Максвела в интегральной форме.

Получим дифференциальную форму этого уравнения, воспоьзуемся уравнением Стокса 1.4.

Применяя 1.4 к левой части 1.9 получим

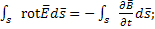(1.10)

Это уравнение справедливо, если равны подинтегральные выражения

rot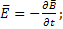(1.10)

Для изображения сред, для которых справедливы соотношения 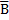=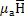. Уравнение 1.10 можно записать

rot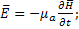(1.10а)

2-е уравнение Максвела означает что переменное во времени магнитное поле вихревое электрическое поле в пространстве.

1.3 Третье и четвертое уравнение Максвела.

Эти уравнения устанавливают источники эл. и магн. полей.

Третье уравнение Максвела есть обобщение з. Гаусса на переменные поля.

Закон. Гаусса: гласит - поток вектора электрического смещения 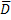через замкнутую поверхность S, охватывающую объем V равен, заряду заключенному в этом объеме т.е.

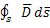=Q; (1.11)

Выразим Q.

Q= 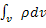; (1.12)

Ρ- объемная плотность заряда

Подставим 1.12 в 1.11 получим

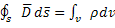; (1.13)

Воспользуемся т. Гаусса- Остроградского. Преобразуем поверхностный интеграл в объем. Эта т. применительна к произвольному вектору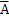

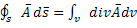; (1.14)

Применим 1.14 к левой части 1.13

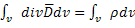; (1.15)

Уравнение 1.15 есть третье уравнение Максвелла в интегральной форме.

Третье уравнение Максвелла в дифференциальной форме получим из уравнения 1.15 из которог следует

div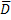=ρ; (1.16)

-3-е уравнение Максвелла в диф-ой форме.

Физ. Смысл: Оно говорит о том что источником эл. поля является эл. заряд

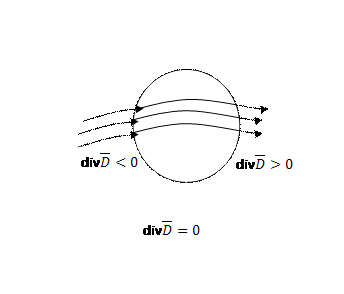
Если дивергенцмя некоторого поля равна нулю, это означает что вектор 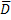замкнут.

Для случая переменных полей уравнение 1.11 принимает вид

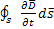; (1.17) Изменения заряда во времени есть сила тока.

Из уравнения 1.16 для переменных полей имеем:

div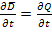

div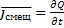; (1.18)

Предположение что в какой то момент времени на обкладках конденцатора распределение зарядов, указанное на рисунке.

Источником тока смещения является заряд из

Изменение заряда во времени всегда является первичным источником эл. поля.

Распространение эл/магн. поля происходит за счет взаимного преобразования эл. магн. энергии.

Четвертое уравнение Максвелла в интегральной форме выражает з. Гаусса для магнитного поля, который утверждает что поток вектора магнитной индукции 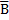через замкнутую поверхность равен нулю.

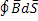; (1.19)

– 4-е уравнение Максвелла в интегральной форме.

Воспользуемся т. Гауса-Острограцкого и получим уравнение в диф-ой форме в виде

div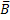=0; (1.20)

-4-е уравнение Максвелла в диф-ой форме.

4-е уравнение Максвелла в диф-ой форме показывает, что магнитные заряды отсутствуют, и магнитное поле всегда замкнуто в пространстве.

Дата добавления: 2014-01-14