Ординарность

Определение 12. Поток событий называется ординарным, если вероятность попадания на элементарный участок времени двух и более событий пренебрежимо мала по сравнению с длиной этого участка.

Замечание. Другими словами, ординарность потока означает, что за малый промежуток времени практически невозможно появление более одного события. Реальные потоки событий либо являются ординарными, либо могут быть достаточно просто приведены к ординарным.

3. Отсутствие последействия.

Определение 13. Поток событий называется потоком с отсутствием последействия, если для любых непересекающихся участков времени количество событий, попадающих на один из них, не зависит от того, сколько событий попало на другие участки времени.

Определение 13. Поток событий, одновременно обладающий свойствами стационарности, ординарности и отсутствия последействия, называется простейшим потоком событий.

Замечание. Для простейшего потока интенсивность .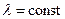

Определение 14. Поток событий называется пуассоновским (потоком Пуассона, стационарным потоком Пуассона), если в нём число событий, происходящих в течение любого фиксированного интервала времени, имеет распределение Пуассона, и ч и сла событий, происходящих в непересекающиеся промежутки времени, независимы.

Напоминание. Распределение Пуассона имеет вид 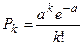, 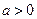– параметр. Математическое ожидание и дисперсия случайной величины, имеющей пуассоновское распределение, равны .

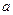Замечание 1. Пуассоновский поток является простейшим потоком событий с интенсивностью 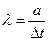для любого промежутка времени 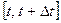. Параметр 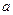можно интерпретировать как среднее число событий, приходящееся на участок времени .

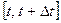Замечание 2. Для простейшего потока событий промежуток времени 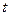между соседними событиями распределён по показательному закону с математическим ожиданием (средним значением) и СКО, равным .

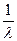Напоминание. Показательное распределение с параметром 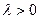имеет плотность распределения вида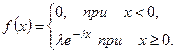

Определение 15. Если поток событий не имеет последействия, ординарен, но не стационарен, то его называют нестационарным пуассоновским потоком.

Замечание 1. В нестационарном пуассоновском поток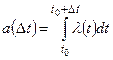е , где 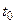– начало участка времени.

Замечание 2. Для нестационарного потока закон распределения промежутка времени 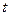между соседними событиями уже не является показательным, так как зависит от положения на оси 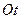и вида зависимости 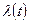. Однако, для некоторых задач при сравнительно небольших изменениях 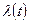его можно считать показательным с интенсивностью .

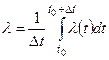Теоретический материал: [5],глава 2.

Дата добавления: 2014-01-14