
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Рассмотрим двойной интеграл
|
|
|
|
 (13)
(13)
Если разбиение области D проводить прямыми, параллельными координатным осям, т.е. координатными линиями декартовой системы координат: x =const, y =const, то
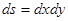 .
.
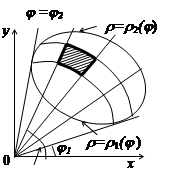 1. Элемент площади в полярной системе координат.
1. Элемент площади в полярной системе координат.
Пусть требуется вычислить интеграл (13) в полярной системе координат, причем полюс совпадает с началом координат и полярная ось совпадает с осью абсцисс.
Тогда декартовы координаты точки выражаются через полярные по формулам:
Рис.24.
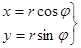 (14)
(14)
Значение интеграла (I3) не зависит от способа разбиения области D на частичные, поэтому разобьём её системой координатных линий полярной системы (рис.24):
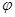 =const (лучи, выходящие из полюса) и
=const (лучи, выходящие из полюса) и 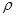 =const (концентрические окружности с центром в полюсе).
=const (концентрические окружности с центром в полюсе).
|
|
|
|
|

|




|
|


|
|
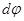 и
и 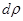 малы), то каждую элементарную площадку можно считать прямоугольником со сторонами
малы), то каждую элементарную площадку можно считать прямоугольником со сторонами 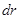 и
и 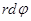 (с точностью до бесконечно малых высшего порядка).
(с точностью до бесконечно малых высшего порядка).
Рис. 25.
Тогда
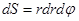 (15)
(15)
элемент площади в полярной системе.
2. Переход в двойном интеграле к полярным координатам.
Чтобы преобразовать интеграл (13) к полярной системе координат, нужно х и у в функции f (x,y) выразить через 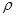 и
и 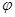 по формулам (14) и взять элемент площади (15):
по формулам (14) и взять элемент площади (15):
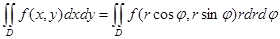 (16)
(16)
Для вычисления двойного интеграла в полярной системе координат его сводят к повторному.
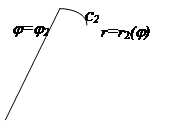 |
|

|


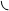

|
 и
и 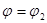 и кривыми
и кривыми 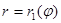 и
и 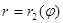 , причём линии
, причём линии  пересекают границу не более чем в двух точках
пересекают границу не более чем в двух точках
Рис.26.
(С 1 и С 2) – точки входа и выхода.
Тогда
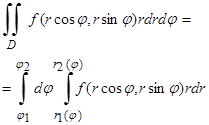 (17)
(17)
|
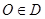 и любой луч
и любой луч  пересекает гра- ницу области только в одной точке (рис.27). Тогда
пересекает гра- ницу области только в одной точке (рис.27). Тогда

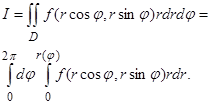 (18)
(18)
Рис. 27.
Замечание. Оба интеграла а формулах (17) и (18) могут иметь постоянные пределы лишь в том случае, когда границей области D служат координатные линии 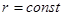 и
и  .
.
Пример 1. Вычислить двойной интеграл
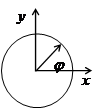 |
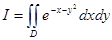 , где
, где
D – круг радиуса 1 с центром в начале координат 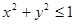 (рис.28).
(рис.28).
Рис. 28.
Перейдем к полярным координатам
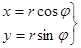
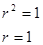 .
.
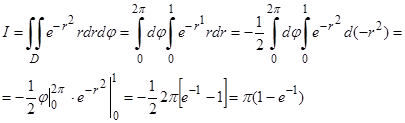
Пример 2. Вычислить двойной интеграл
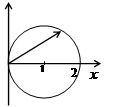
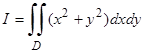
D: 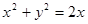
Перейдем к полярным
координатам по формулам (14)
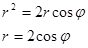 Рис. 29
Рис. 29
Полученное уравнение описывает окружность с центром в точке (1,0) и радиуса 1 (рис. 29).
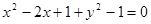
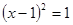
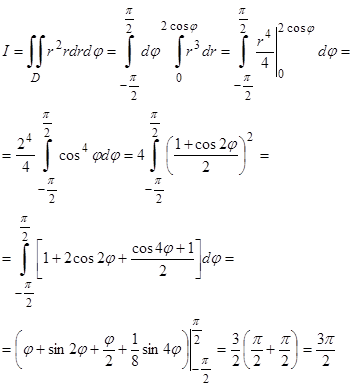
9.5.Приложения двойных интегралов.
Двойные интегралы применяются для вычисления площадей плоских фигур и поверхностей, объемов пространственных тел, механических величин связанных с непрерывным распределением массы в плоской области, а также для решения многих других задач.
Геометрические приложения двойных интегралов
1. Площадь 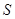 области
области 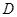 на плоскости
на плоскости 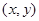 выражается формулой
выражается формулой 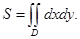
2. Объем 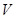 тела
тела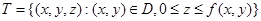 , где
, где
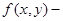 непрерывная неотрицательная в области
непрерывная неотрицательная в области 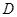
функция, выражается формулой 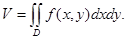
Физические приложения двойных интегралов
Пусть 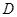 - материальная бесконечно тонкая пластинка с плотностью
- материальная бесконечно тонкая пластинка с плотностью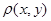 . Тогда справедливы следующие формулы:
. Тогда справедливы следующие формулы:
1.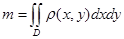 - масса пластинки;
- масса пластинки;
2. 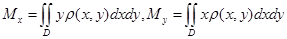 - статические моменты пластинки относительно осей
- статические моменты пластинки относительно осей 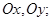
3.  - координаты центра тяжести пластинки;
- координаты центра тяжести пластинки;
4. 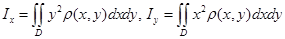 - моменты инерции пластинки относительно осей
- моменты инерции пластинки относительно осей 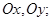
5. 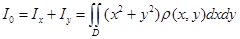 - момент инерции пластинки относительно начала координат.
- момент инерции пластинки относительно начала координат.
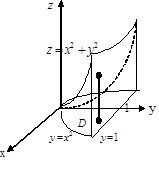 Пример. Найти объем тела
Пример. Найти объем тела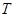 , ограниченного поверхностями
, ограниченного поверхностями
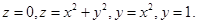
Решение. Данное тело можно представить в виде
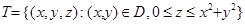 ,
,
где 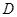 - область на плоскости
- область на плоскости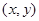 , ограниченная кривыми
, ограниченная кривыми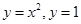 , то есть
, то есть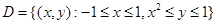 . Переходя от двойного интеграла к повторному, получим
. Переходя от двойного интеграла к повторному, получим

Пример. Найти моменты инерции 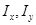 относительно осей
относительно осей 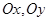 пластины с плотностью
пластины с плотностью 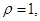 ограниченной кривыми
ограниченной кривыми 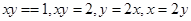 и расположенной в первом квадранте.
и расположенной в первом квадранте.
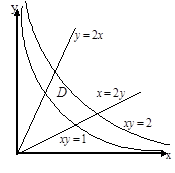 Решение.
Решение. 
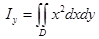 . Чтобы свести каждый из этих интегралов к повторному, нужно область
. Чтобы свести каждый из этих интегралов к повторному, нужно область 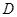 разбить на три части. Удобнее перейти к полярным координатам:
разбить на три части. Удобнее перейти к полярным координатам: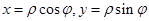 . Тогда
. Тогда 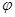 изменяется от
изменяется от 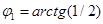 до
до , а при каждом значении
, а при каждом значении 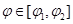 переменная
переменная 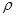 изменяется от
изменяется от 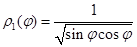 (значение
(значение 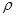 на кривой
на кривой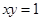 , уравнение которой в полярных координатах в I квадранте имеет вид
, уравнение которой в полярных координатах в I квадранте имеет вид  ) до
) до 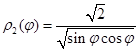 (значение
(значение 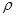 на кривой
на кривой 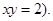 Следовательно,
Следовательно,
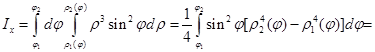
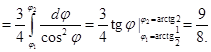

Аналогично получаем 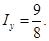
Задачи для самостоятельного решения
1. Свести двойной интеграл  к повторному двумя способами, если:
к повторному двумя способами, если:
а) 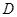 - область, ограниченная кривыми
- область, ограниченная кривыми 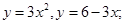
б) 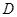 - круг
- круг 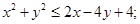
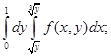
в) 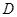 - треугольник со сторонами, лежащими на прямых
- треугольник со сторонами, лежащими на прямых 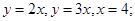
г) 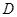 - кольцо
- кольцо 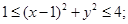
д) 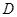 - область, ограниченная кривыми
- область, ограниченная кривыми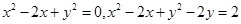 ;
;
е) 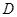 - область, лежащая вне окружности и внутри кривой
- область, лежащая вне окружности и внутри кривой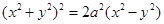 .
.
2. Изменить порядок интегрирования в повторных интегралах:
а) б)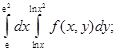 в)
в)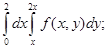
г)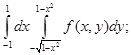 д)
д) 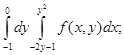
е) 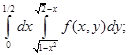 ж)
ж) 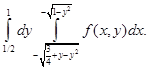
3. Вычислить двойные интегралы:
а)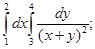 б)
б) 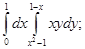
в) 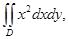 где
где 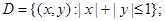
г) 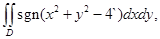 где
где 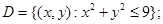
д) 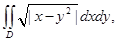 где
где 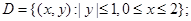
е)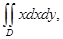 где
где 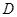 - область, ограниченная кривыми
- область, ограниченная кривыми
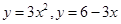 ;
;
ж) 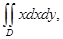 где
где 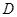 - область, ограниченная кривой
- область, ограниченная кривой 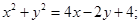
з) 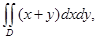 где
где 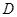 - область, ограниченная кривыми
- область, ограниченная кривыми 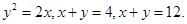
4. В следующих интегралах перейти к полярным координатам
а)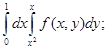 б)
б) 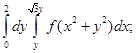
в)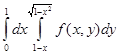 .
.
5. Вычислить объем тела, ограниченного поверхностями:
а)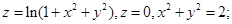
б) 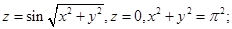
в) 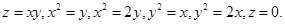
6. Найти координаты центра тяжести однородной пластинки, ограниченной кривыми:
а) 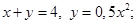
б) 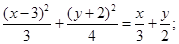
в) 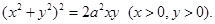
Ответ: а) 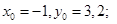 б)
б)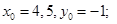
в)
7. Найти координаты центра тяжести круглой пластинки 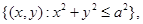 если ее плотность в точке
если ее плотность в точке  пропорциональна расстоянию от точки
пропорциональна расстоянию от точки  до точки
до точки 
Ответ: 
8. Найти моменты инерции 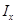 и
и 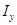 относительно осей
относительно осей 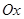 и
и 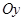 однородной пластинки с плотностью
однородной пластинки с плотностью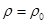 , ограниченной кривыми:
, ограниченной кривыми:
а) 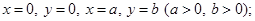
б) 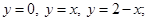
в) 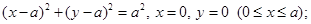
г)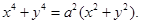
Ответ: а)  б)
б)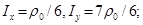 в)
в) 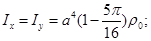 г)
г)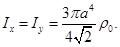
9. Найти моменты инерции 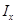 и
и 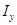 относительно осей
относительно осей 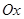 и
и 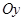 однородной пластинки с плотностью
однородной пластинки с плотностью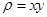 , ограниченной кривыми:
, ограниченной кривыми:
а) 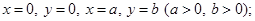
б) 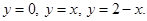
Ответ: а)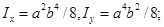 б)
б) 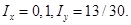
Ответ: Взяв ось 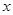 в качестве оси абсцисс, получаем
в качестве оси абсцисс, получаем 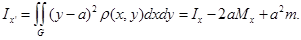 Так как, по условию
Так как, по условию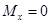 , то приходим к равенству
, то приходим к равенству 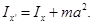
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 966; Нарушение авторских прав?; Мы поможем в написании вашей работы!