Применение интегрального соотношения для расчета турбулентного пограничного слоя на плоской пластине

Лекция 10

Интегральное соотношение Кармана и рассмотренная выше методика расчета характеристик пограничного слоя может быть применена и для расчета турбулентного пограничного слоя на поверхности пластины, поскольку при выводе интегрального соотношения Кармана не делалось никаких предположений о характере течения жидкости в пограничном слое. Имеются два отличия в выводе уравнения для толщины пограничного слоя: иная зависимость 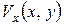(рис. 4.8) и другая методика определения касательного напряжения .

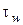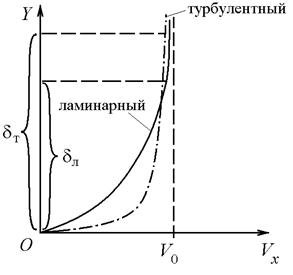
Рис. 4.8. Профили скорости в ламинарном и турбулентном пограничном слоях:

- ламинарный пограничный слой;

- турбулентный пограничный слой

При определении профиля скорости 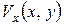в турбулентном погранич­ном слое на пластине, как правило, используют степенную зависимость:

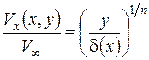, (4.15)

где - толщина пограничного слоя, .

Если скорость невозмущенного потока не превышает половины скорости звука, то полагают n = 7 (получается так называемый ²закон 1/7²). Таким образом, скорость потока около поверхности стенки при турбулентном режиме течения с ростом координаты y, изменяется более быстро, по сравнению с ламинарным режимом течения, а профиль скорости имеет более наполненный вид (рис. 4.8). Следовательно, производная в турбулентном пограничном слое выше, чем в ламинарном. Согласно закону трения Ньютона (4.8), можно ожидать, что касательное напряжение в турбулентном пограничном слое выше, чем в ламинарном.

Для получения обыкновенного дифференциального уравнения, определяющего толщину пограничного слоя , необходимо подставить выражение для (оно следует из (4.15)) в интегральное соотношение Кармана (4.4) на пластине. Имеем

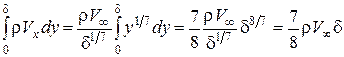; (4.16)

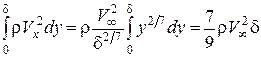. (4.17)

Закон трения Ньютона при профиле скорости, соответствующем ²закону 1/7², использовать для расчета касательного напряжения нельзя, т.к. значение касательного напряжения на стенке получается равным бесконечности (²закон 1/7² около поверхности стенки не справедлив). Поэтому приближенная оценка проводится для касательного напряжения, полученного в теории течения жидкости в гладких трубах:

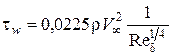, (4.18)

где .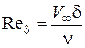

Подставляя выражения (4.16), (4.17), (4.18) в интегральное соотношение Кармана, получим выражение:

,

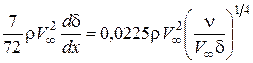После интегрирования имеем:

.

Так как, при , то C = 0, откуда

. (4.19)

Подставляя выражение (4.19) в (4.18), можно получить формулу для определения касательного напряжения

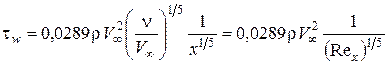. (4.20)

Таким образом, толщина турбулентного пограничного слоя пропорциональна (почти линейная зависимость). В сравнении с ламинарным пограничным слоем 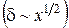толщина турбулентного пограничного слоя растет значительно быстрее. Напротив, касательное напряжение на поверхности пластины в турбулентном пограничном слое пропорционально и, по сравнению с ламинарным пограничным слоем 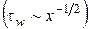, изменяется значительно медленнее.

Определим силу трения 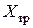на поверхности плоской пластины в турбулентном пограничном слое. Как и для ламинарного течения, возьмем пластину длиной b и шириной 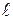. В результате преобразований получим

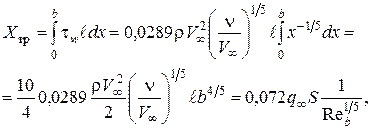(4.21)

Следовательно, коэффициент сопротивления трения будет определяться выражением

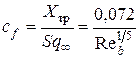. (4.22)

Для построения графической зависимости коэффициента трения от числа Рейнольдса 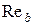(рис. 4.9), удобно выражения (4.14) и (4.22) представить в логарифмической форме:

,

.

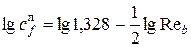Рис. 4.9. Зависимость коэффициента сопротивления трения плоской пластины от числа Рейнольдса

Из графика (рис. 4.9) видно, что коэффициент трения при смене режима течения резко возрастает. При этом коэффициент трения уменьшается с ростом числа Рейнольдса, как для ламинарного, так и для турбулентного течения. Однако для турбулентного режима течения коэффициент трения падает не столь интенсивно.

Контрольные вопросы

1. Чем отличаются профили скорости 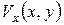для ламинарного и турбулентного пограничного слоя?

2. С каким из критериев подобия связан коэффициент трения?

3. Чем отличаются зависимости толщины пограничного слоя и касательного напряжения от координаты x для ламинарного и турбулентного пограничного слоя?

4. Как изменяется касательное напряжение на поверхности пластины при переходе через критическое число Рейнольдса?

5. Можно ли использовать профиль скорости, соответствующий ²закону 1/7² при вычислении касательного напряжения на поверхности пластины?

6. Можно ли использовать полином при подстановке в интегральное соотношение Кармана для турбулентного пограничного слоя?

Дата добавления: 2014-01-14