Математическая сторона задачи

Физическая сторона задачи

Учитывая, что, в соответствии с гипотезой об отсутствии боковых давлений, σy=σz=0, запишем закон Гука для изгиба в виде

Из формулы (10.6) с учетом (10.5), получим закон распределения нормальных напряжений по сечению балки:

Подставляя (10.7) в каждое из уравнений (10.4), имеем следующие соотношения:

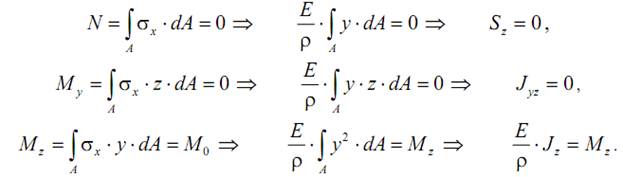
Из анализа первого и второго полученных выражений следует, что оси y и z являются главными центральными осями сечения, а нейтральная ось проходит через центр тяжести сечения.

Из последнего равенства получим формулу для определения кривизны бруса

(1/ρ) при изгибе

подставляя которую в выражение (10.7), получим формулу определения нормальных напряжений при изгибе:

Из анализа полученного уравнения следует, что нормальные напряжения при изгибе равны нулю в точках, лежащих на нейтральной оси, и достигают экстремальных значений на поверхности балки, при y=|y|max.

Максимальные нормальные напряжения при изгибе найдем по формуле:

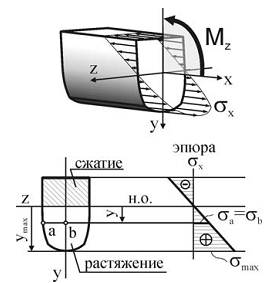где Wz – осевой момент сопротивления

Таким образом, в случае изгиба условие прочности по нормальным напряжениям может быть записано в следующем виде (для материала балки, одинаково сопротивляющегося растяжению-сжатию):

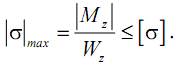
10.5. Касательные напряжения при поперечном изгибе прямого бруса

При плоском поперечном изгибе, когда в сечениях балки действуют и изгибающий момент M и поперечная сила Q, возникают не только нормальные σ, но и касательные напряжения τ.

Нормальные напряжения при поперечном изгибе рассчитываются по тем же формулам, что и при чистом изгибе:

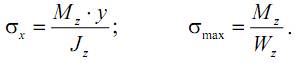
Далее получим зависимости для определения касательных напряжений τ в случае поперечного изгиба балки.

При выводе формулы примем некоторые гипотезы, которые сделают данную задачу статически определимой:

1) касательные напряжения, действующие на одинаковом расстоянии y от нейтральной оси, постоянны по ширине бруса;

2) касательные напряжения всюду параллельны силе Q.

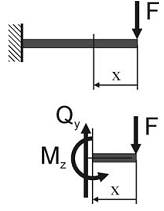
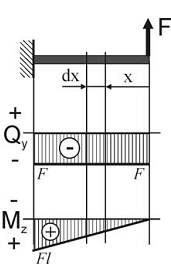Рассмотрим консольную балку, находящуюся в условиях поперечного изгиба под действием силы F. Построим эпюры внутренних усилий Qy и Mz.

На расстоянии x от свободного конца балки выделим элементарный участок балки abcd длиной dx и шириной, равной ширине балки b. Покажем внутренние усилия, действующие по граням элемента: на грани cd возникает поперечная сила Qy и изгибающий момент Mz, а на грани ab – также поперечная сила Qy и изгибающий момент Mz+dM (так как Qy остается постоянной по длине балки, а момент Mz изменяется, см. эпюру).

На расстоянии y от нейтральной оси отсечем часть элемента abcd, покажем напряжения, действующие по граням полученного элемента mbcn, и рассмотрим его равновесие. На гранях, являющихся частью наружной поверхности балки, нет напряжений. На боковых гранях элемента от действия изгибающего момента Mz возникают нормальные напряжения σ* и σ**, причем

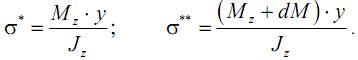
Кроме того, на этих гранях от действия поперечной силы Qy возникают касательные напряжения τ, такие же напряжения возникают по закону парности касательных напряжений и на верхней грани элемента.

Составим уравнение равновесия элемента mbcn, проецируя равнодействующие рассмотренных напряжений на ось x:

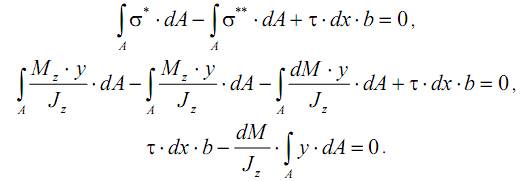
Выражение, стоящее под знаком интеграла, представляет собой ни что иное, как статический момент боковой грани элемента mbcn относительно оси z, поэтому можем записать

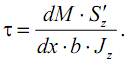
Учитывая, что, согласно дифференциальным зависимостям Журавского Д. И. при изгибе,

выражение для касательных напряжений при поперечном изгибе τ можем переписать следующим образом (формула Журавского)

Проанализируем формулу Журавского (10.10). Здесь Q≡Qy – поперечная сила в рассматриваемом сечении; Jz – осевой момент инерции сечения относительно оси z; b – ширина сечения в том месте, где определяются касательные напряжения; zS′ – статический момент относительно оси z части сечения, расположенной выше (или ниже) того волокна, где определяется касательное напряжение τ:

здесь и А′ – координата центра тяжести и площадь рассматриваемой части сечения, соответственно.

10.6. Полная проверка прочности. Опасные сечения и опасные точки

Для проверки на прочность при изгибе по действующим на балку внешним нагрузкам строят эпюры изменения внутренних усилий (Mz, Qy) по ее длине и определяют опасные сечения балки, для каждого из которых необходимо провести проверку прочности.

При полной проверке прочности таких сечений будет, как минимум, три (иногда они совпадают):

1) сечение, в котором изгибающий момент Mz достигает своего максимального по модулю значения, – именно по этому сечению подбирают сечение всей балки;

2) сечение, в котором поперечная сила Qy достигает своего максимального по модулю значения;

3) сечение, в котором и изгибающий момент Mz и поперечная сила Qy достигают по модулю достаточно больших величин.

В каждом из опасных сечений необходимо, построив эпюры нормальных и касательных напряжений, найти опасные точки сечения (проверка прочности проводится для каждой из них), которых также будет, как минимум, три:

1) точка, в которой нормальные напряжения σx достигают своего максимального значения, – то есть точка на наружной поверхности балки наиболее удаленная от нейтральной оси сечения;

2) точка, в которой касательные напряжения τxy достигают своего максимального значения, – точка, лежащая на нейтральной оси сечения;

3) точка, в которой и нормальные напряжения σx и касательные напряжения τxy достигают достаточно больших величин (эта проверка имеет смысл для сечений типа тавра или двутавра, где ширина резко изменяет свое значение).

Дата добавления: 2014-01-14