
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Свойства поверхностного интеграла
|
|
|
|
Зависимость между поверхностными интегралами первого и второго рода
Известно, что 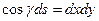 ,
,  ,
, 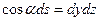 .
.

Интеграл стоящий в правой части называется поверхностным интегралом второго рода по координатам.
1)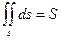 ,
, 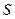 - площадь поверхности
- площадь поверхности
2)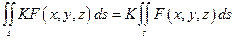
3)
4) Если поверхность 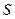 разбита на части, то поверхностный интеграл по всей поверхности равен сумме интегралов по ее частям.
разбита на части, то поверхностный интеграл по всей поверхности равен сумме интегралов по ее частям.
5) Если  , то
, то 
6)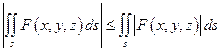 .
.
7)Теорема о среднем в поверхностном интеграле: Если функция  непрерывна на поверхности
непрерывна на поверхности 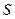 , то найдется, по крайней мере одна точка
, то найдется, по крайней мере одна точка  , лежащая на поверхности
, лежащая на поверхности 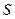 , то
, то  , где
, где 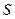 - площадь данной поверхности.
- площадь данной поверхности.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 349; Нарушение авторских прав?; Мы поможем в написании вашей работы!