Дивергенция векторного поля

Пусть векторное поле задано вектором 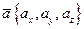. Будем рассматривать его как поле текущей жидкости. Поток вектора через некоторую поверхность 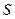в данном вектором поле может быть положительным 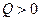, это значит, что имеется источник. Если 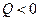, то в выделенном объеме имеются стоки. Если 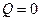, то в выделенном объеме нет ни источников ни стоков, или их мощности таковы, что они компенсируют друг друга. Поэтому для характеристики потока вводят понятие мощности, то есть такое количество жидкости, которое протекает через поверхность в единицу времени.

Плотность источника определяется по формуле:

.

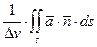Чтобы определить плотность источника в точке следует перейти к пределу когда объем стягивается в точку и этот предел называется дивергенцией (расходимостью векторного поля).

.

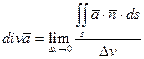Дивергенция величина скалярная и вычисляется по формуле:

.

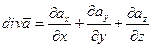Если дивергенция равна 0, то поле называется соленоидальным.

Пример. Вычислить дивергенцию поля линейных скоростей.

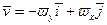
Решение

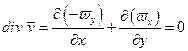
Дата добавления: 2014-01-14