
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Системы линейных дифференциальных уравнений с постоянными коэффициентами
|
|
|
|
Однородные системы. Решение системы предполагает, что мы должны найти  функций
функций  , удовлетворяющих уравнениям
, удовлетворяющих уравнениям

Заметим, что в системах мы будем рассматривать только дифференциальные уравнения первого порядка. В противном случае, если в системе появляется, например, производная  , мы вводим новую функцию
, мы вводим новую функцию  , обозначаем
, обозначаем 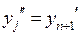 и добавляем еще одно уравнение системы:
и добавляем еще одно уравнение системы:  .
.
Для упрощения выкладок мы исследуем случай  . Полученные результаты легко обобщаются на случай произвольного
. Полученные результаты легко обобщаются на случай произвольного  . Введенную выше линейную однородную систему можно свести к линейному однородному дифференциальному уравнению высокого порядка с постоянными коэффициентами. Покажем, как это делается для случая
. Введенную выше линейную однородную систему можно свести к линейному однородному дифференциальному уравнению высокого порядка с постоянными коэффициентами. Покажем, как это делается для случая  . Пусть нам нужно решить систему
. Пусть нам нужно решить систему

Продифференцируем первое уравнение и выразим в полученной правой части  через правую часть второго уравнения. Мы получим
через правую часть второго уравнения. Мы получим
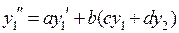 . А теперь входящую в полученную правую часть функцию
. А теперь входящую в полученную правую часть функцию 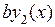 заменим ее выражением из первого уравнения исходной системы:
заменим ее выражением из первого уравнения исходной системы: 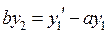 . Мы получили линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно функции
. Мы получили линейное однородное дифференциальное уравнение второго порядка с постоянными коэффициентами относительно функции 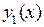 :
:
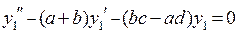 .
.
Мы знаем, что решение этого уравнения представляет собой линейную комбинацию частных решений, которые строятся с помощью корней характеристического уравнения. Поэтому и решение заданной системы из двух уравнений с двумя неизвестными функциями, не приводя ее к решению линейного уравнения второго порядка, будем искать в виде линейной комбинации функций вида  .
.
Попробуем найти решение системы из двух дифференциальных уравнений, не сводя ее к уравнению второго порядка, в виде  . Подставим эти функции в систему и сократим оба уравнения на
. Подставим эти функции в систему и сократим оба уравнения на  . Мы получим алгебраическую систему из двух уравнений
. Мы получим алгебраическую систему из двух уравнений
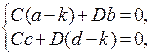
относительно неизвестных констант  и
и  . Как известно из курса алгебры, однородная линейная алгебраическая система имеет только нулевые решения, если главный определитель системы отличен от нуля. Следовательно, чтобы получить нетривиальные решения, мы должны приравнять определитель этой системы нулю. Таким образом, число
. Как известно из курса алгебры, однородная линейная алгебраическая система имеет только нулевые решения, если главный определитель системы отличен от нуля. Следовательно, чтобы получить нетривиальные решения, мы должны приравнять определитель этой системы нулю. Таким образом, число 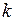 должно быть корнем уравнения
должно быть корнем уравнения
 ,
,
называемого характеристическим уравнением системы

После того, как мы определим значения 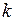 (два значения в соответствии с основной теоремой алгебры), связь между коэффициентами
(два значения в соответствии с основной теоремой алгебры), связь между коэффициентами  и
и  определится, например, из соотношения
определится, например, из соотношения  . Очевидно, что при различных значениях числа
. Очевидно, что при различных значениях числа 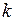 мы получим различные соотношения между коэффициентами
мы получим различные соотношения между коэффициентами  и
и  . Получив два частных решения с произвольными коэффициентами, мы сложим их и получим общее решение.
. Получив два частных решения с произвольными коэффициентами, мы сложим их и получим общее решение.
П р и м е р. Решить систему
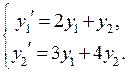
Решим характеристическое уравнение  . Оно имеет два различных корня:
. Оно имеет два различных корня: 
 . При
. При  мы имеем следующую связь между
мы имеем следующую связь между  и
и  :
:  . При
. При  получим:
получим:  . Обозначив через
. Обозначив через  коэффициент при
коэффициент при  , а через
, а через 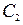 – коэффициент при
– коэффициент при  в выражении
в выражении 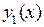 , мы получим общее решение:
, мы получим общее решение:  ,
, 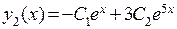 .
.
Заметим, что не обязательно находить связь между  и
и  , а можно, получив общее решение для
, а можно, получив общее решение для 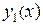 , найти общее решение для
, найти общее решение для  из первого уравнения системы. В данном случае, зная
из первого уравнения системы. В данном случае, зная  , можно найти
, можно найти  .
.
Возникает вопрос: в каком виде брать решение, если характеристическое уравнение имеет либо кратные, либо комплексные корни? Руководствуясь тем, что решение системы равносильно решению линейного однородного уравнения второго порядка, возьмем частные решения в соответствующем виде. Так, в случае, когда мы получим единственный корень  кратности два, функции, дающие решения системы примут вид
кратности два, функции, дающие решения системы примут вид  , а в случае, когда корнями характеристического уравнения являются комплексные числа
, а в случае, когда корнями характеристического уравнения являются комплексные числа 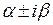 , решения системы примут вид
, решения системы примут вид  . Естественно, что коэффициенты при частных решениях двух функций зависят друг от друга.
. Естественно, что коэффициенты при частных решениях двух функций зависят друг от друга.
П р и м е р. Решить систему 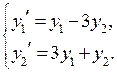 Характеристическим уравнением системы является уравнение
Характеристическим уравнением системы является уравнение  . Корни характеристического уравнения:
. Корни характеристического уравнения:  . Поэтому
. Поэтому  . Теперь из первого уравнения системы найдем
. Теперь из первого уравнения системы найдем  .
.
П р и м е р. Решить систему  Характеристическим уравнением этой системы будет
Характеристическим уравнением этой системы будет  . Корнем этого уравнения кратности два является число 3. Поэтому мы решение запишем в виде
. Корнем этого уравнения кратности два является число 3. Поэтому мы решение запишем в виде 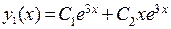 Используем первое уравнение системы для получения
Используем первое уравнение системы для получения  .
.
Неоднородные системы. В случае неоднородной системы в правой части каждого из уравнений системы появляется произвольная функция:

Очевидно, что для получения общего решения неоднородной системы достаточно найти частное решение неоднородной системы и сложить его с общим решением соответствующей однородной системы. Мы будем искать решение неоднородной системы методом вариации произвольной постоянной на примере системы из двух уравнений с двумя неизвестными функциями.
Пусть нам нужно решить систему
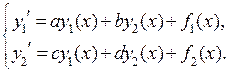
Общим решением соответствующей однородной системы являются функции  , причем
, причем  линейно выражаются через
линейно выражаются через 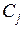 ,
,  . Заметим, что справедливы соотношения
. Заметим, что справедливы соотношения
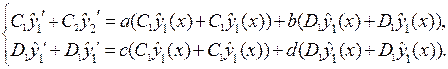
Ищем решение неоднородной системы в виде
 . Подставим эти функцию в неоднородную систему и воспользуемся предыдущей системой, тогда получим систему
. Подставим эти функцию в неоднородную систему и воспользуемся предыдущей системой, тогда получим систему

в которой  линейно выражены через
линейно выражены через  ,
,  . Таким образом, мы получаем линейную систему относительно
. Таким образом, мы получаем линейную систему относительно  ,
,  . Восстановив функции
. Восстановив функции 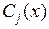 ,
,  , с точностью до произвольных слагаемых, мы получим требуемое решение.
, с точностью до произвольных слагаемых, мы получим требуемое решение.
П р и м е р. Решить систему

Решим характеристическое уравнение для однородной системы: 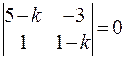 . Корнями этого уравнения являются числа
. Корнями этого уравнения являются числа 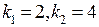 . Поэтому за общее решение однородной системы можно взять функции
. Поэтому за общее решение однородной системы можно взять функции 
Теперь общее решение неоднородной системы возьмем в виде
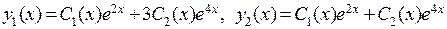 . Для определения функций
. Для определения функций 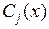 ,
,  , решим систему
, решим систему
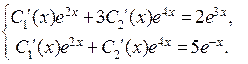
Получим  . В итоге получим общее решение неоднородной системы:
. В итоге получим общее решение неоднородной системы:  .
.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 603; Нарушение авторских прав?; Мы поможем в написании вашей работы!