Теорема. Основные гуморальные факторы неспецифической резистентности факторы источник результат ионы и низкомолекулярные соединения

ОСНОВНЫЕ ГУМОРАЛЬНЫЕ ФАКТОРЫ НЕСПЕЦИФИЧЕСКОЙ РЕЗИСТЕНТНОСТИ

ФАКТОРЫ	ИСТОЧНИК	РЕЗУЛЬТАТ
Ионы и низкомолекулярные соединения
Снижение рО2 в тканях; супероксидные кислородные продукты (ОН^-, О2^-, Н2О2)	Фагоциты, иногда бактерии	Снижение содержания О2 угнетает рост многих бактерий; супероксиды проявляют антимикробный эффект
Ионы галогенов (преимущественно Cl^-)	Тканевые жидкости	Cl^- взаимодействует с миелопероксидазой и Н2О2, проявляя антимикробное действие
Ионы Н^+	Фагоциты и другие клетки	В высоких концентрациях проявляют антимикробный эффект
Жирные кислоты	Метаболиты фагоцитов и других клеток	Проявляют антимикробный эффект при низких значениях рН
Фактор активации тромбоцитов	Фагоциты и другие клетки	Вызывает агрегацию и дегрануляцию тромбоцитов, активирует макрофаги и ингибирует пролиферацию Т-клеток
Простые белковые молекулы
Лактоферрин	ПМЯЛ	Подавляет рост бактерий, связывая Fe^+
Трансферрин	Печень	Подавляет рост бактерий, связывая Fe^+
Цитокины (ИЛ, ФНО, ИФН)	Клетки макрофагально-моноцитарной системы	Ингибирую размножение вирусов (ИФН), вызывают развитие лихорадочной реакции (ИЛ1); стимулируют образование белков острой фазы воспаления (ИЛ1, ИЛ6, ФНО); повышают адгезивность эндотелия (ИЛ1), являются хемоаттрактантами (ИЛ8)
Лизоцим	Фагоциты	Проявляет множественное антимикробное действие, гидролизуя муреин
Фибронектин	Макрофаги, фибробласты	Опсонизирует стафилококки
Сложные белковые системы
Система комплемента	Макрофаги, гепатоциты	Повышает проницаемость сосудов, вызывает спазм гладкой мускулатуры, проявляет бактерицидный эффект, действует как хемоаттрактант и опсонин
Свертывающая система крови	Печеночные кининогены, трансформированныеспецифическими протеазами (калликоеинами)	Повышает проницаемость сосудов и вызывает их дилатацию, обусловливает проявление болевого синдрома
Фибринопептиды	Фибриноген	Проявляют свойства хемоаттрактантоа и опсонина
Фактор Хагемана	Печень, свертывающий каскад	Пусковой фактор для многих реакций, обусловливающих нарушение кровоснабжения в очаге воспаления.

Всякий многочлен f(x) cтепени n > 0 с действительными коэффициентами раскладывается на множители 1-ой или 2-ой степени также с действительными коэффициентами:

f(x) = a_n∙(x – x₁)∙(x – x₂)∙…∙(x – x_m)∙(x² + p₁x + q₁)∙…∙(x² + p_kx + q_k),

где n = m + 2k, квадратные трёхчлены x² + p_jx + q_j, j = 1,…,k, имеют отрицательный дискриминант.

Док-во. По доказанной выше лемме, все комплексные корни f(x) можно сгруппировать парами комплексно-сопряжённых. Тогда все корни f(x) можно записать списком:

x₁, x₂ ,…, x_m – действительные корни;

z₁, z₁*, z₂, z₂*,…, z_k, z_k* - комплексные корни.

Тогда по следствию из «основной» теоремы имеем:

f(x) = a_n∙(x – x₁)∙(x – x₂)∙…∙(x – x_m)∙(x - z₁)∙(x - z₁*)∙(x - z₂)∙(x - z₂*) ∙…∙(x - z_k)∙(x - z_k*).

Рассмотрим произведение

(x – z_j)∙(x – z_j*) = x² - (z_j + z_j*)∙x + z_j ∙z_j*.

Если z_j = a_j + b_j∙i, z_j* = a_j - b_j∙i, то

z_j + z_j* = 2∙a_j = p_j – действительное число,

z_j ∙z_j* = a_j² + b_j² = q_j – тоже действительное число.

Значит, (x – z_j)∙(x – z_j*) = x² - p_j∙x +q_j – многочлен с действительными коэффициентами и отрицательным дискриминантом, так как его корни комплексные.

Подставляя для всех j = 1,…,k выражения (x – z_j)∙(x – z_j*) = x² - p_j∙x +q_j в выражение для f(x), получим то, ч.т.д.

Примеры:

1) Разложить на множители многочлен f(x) = x⁴ + x² + 1.

Решая биквадратное уравнение, находим корни:

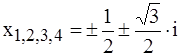. Далее, разбиваем их на пары комплексно-сопряжённых и применяем доказанную выше теорему. Получим

x⁴ + x² + 1 = (х² + х + 1)∙(х² - х + 1).

2) Найти все корни многочлена х⁶ – 2.3х⁵ + х⁴ – х² + 7, применяя MATHCAD.

Решение:

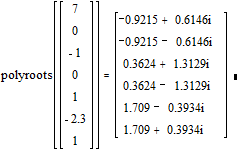
3) Найти все корни многочлена х⁵ – 2.3∙х⁴ + (1 - i)∙х³ – х² + i, применяя MATHCAD.

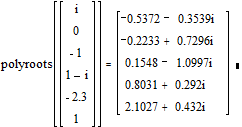Решение:

Из примеров 2) и 3) видно действие последней доказанной теоремы: в примере 2) корни записаны парами комплексно-сопря-жённых, так как многочлен имеет только действительные коэффициенты; в примере 3) нет такой закономерности, так как многочлен имеет комплексные коэффициенты.

Дата добавления: 2014-01-14