Модель управления запасами при вероятностном стационарном спросе и мгновенных поставках

Простейшим случаем УЗ при вероятностном спросе является однократное принятие решения на пополнение запаса. Практическими примерами таких ситуаций являются все однократные процессы с относительно небольшой потребностью в материалах и оборудовании, а также снабжение потребителей в труднодоступных и удаленных районах (например, арктические рейсы).

Пусть z - запас продукции до начала пополнения (известная величина), y - запас после пополнения (), v=y-z- объем заказа на пополнение, x - случайный спрос за время операции Т, f(x) - плотность распределения спроса, функция c(y-z) - расходы на пополнение запаса.

В момент реализации объема пополнения конкретное значение x неизвестно, но задана плотность f(x). Предполагается, что заказ на пополнение исполняется мгновенно.

Если к концу операции на складе остается часть невостребованного запаса (y-x)>0, то система снабжения несет избыточные расходы на хранение, задаваемые функцией . При 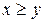функция =0.

При неполном удовлетворении спроса (x>y) система платит штраф .

Тогда математическое ожидание суммарных расходов будет равно:

(1)

Теперь можно поставить следующую задачу:

(2)

(3)

Таким образом, нужно найти такое значение y, которое минимизирует функцию (2) при ограничении (3). Для этого можно найти точки минимума без учета ограничения (3), а потом выбрать те, которые удовлетворяют (3). Те решения, которые получаются из уравнения (точки экстремума)

(4)

И которым соответствуют положительная вторая производная (точки минимума):

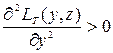(5)

дадут локальные точки минимума функции (2).

В общем случае график для фиксированного значения z имеет несколько локальных минимумов:

Обозначим через y₁ -глобалную точку минимума, через y₃ - глобальную точку минимума в области y>y₁, y₅ - глобальная точка минимума в области y>y₃ т.д. Очевидно, что y₃ - наименьшая из локальных точек минимума без учета y₁ и расположена правее этой точки. Обозначим точку y₂, которая удовлетворяет условиям: y₁<y₂<y₃, . Аналогично вводятся точки y₃<y₄<y₅, и т.д. Пусть введенные величины найдены: , 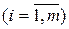. Теперь можно указать оптимальную стратегию управления запасами:

1. Если z<y₁, то нужно заказать продукцию в объеме v=y₁-z. Таким образом, уровень запаса доводится до y₁, который минимизирует общие затраты.

2. Если , то ничего не нужно заказывать, так как и любой заказ ухудшит общие затраты.

3. Если 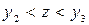, то нужно заказать v=y₃-z. В этом случае значение целевой функции уменьшается до .

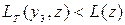4. Если , то ничего не нужно заказывать, так как значение целевой функции возрастает: .

5. И так далее.

Таким образом, при 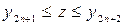, заказ не нужно делать, а при нужно заказать .

Дата добавления: 2014-01-14