Групповая скорость

Строго монохроматическая волна вида

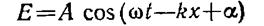(13.6)

представляет собой бесконечную во времени и в пространстве последовательность «горбов» и «впадин», перемещающихся вдоль оси Х с фазовой скоростью, которая описывает перемещение фазы в пространстве в единицу времени, т.е. 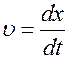,где x- расстояние между точками с одинаковыми фазами. Тогда

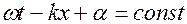(13.7)

Продифференцируем (13.7)

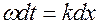, отсюда фазовая скорость зависит от частоты колебаний вектора напряженности электрического поля и волнового числа k

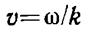(13/8)

С помощью гармонической волны нельзя передать никакого сигнала, так как каждый последующий «горб» ничем не отличается от предыдущего. Для передачи сигнала нужно на волне сделать «отметку», скажем, оборвав ее на некоторое время А/.

Однако в этом случае волна уже не будет описываться уравнением Dt.

Проще всего передать сигнал с помощью светового импульса (рис. 143.1).

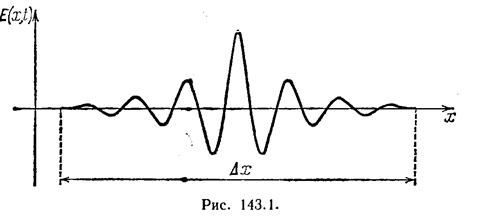
Согласно теореме Фурье подобный импульс можно представить, как наложение волн вида (13.6)), с частотами, заключенными в некотором интервале Dw. Суперпозиция волн, мало отличающихся друг от друга по частоте, называется волновым пакетом или группой волн. Аналитическое выражение для группы волн имеет вид

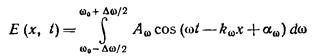(13.9)

(индекс w при A, k и a указывает на то, что эти величины для разных частот различны). При фиксированном t график функции 13.9 имеет вид, оказанный на рис. 143.1. С изменением t график смещается вдоль оси х. В пределах пакета плоские волны в большей или меньшей степени усиливают друг друга, вне пакета они практически полностью гасят друг друга. Соответствующий расчет дает, что чем меньше ширина пакета Dх, тем больший интервал частот Dw. или соответственно больший интервал волновых чисел Dk требуется для того, чтобы описать пакет с помощью выражения 13.9. Имеет место соотношение

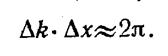
Подчеркнем, что для того, чтобы суперпозицию волн, описываемую выражением 13.9 можно было считать группой волн, необходимо соблюдение условия Dw.<w..

В недиспергирующей среде все плоские волны, образующие пакет, распространяются с одинаковой фазовой скоростью u. Очевидно, что в этом случае скорость движения пакета совпадает с u и форма пакета со временем не изменяется. Можно показать, что в диспергирующей среде пакет с течением времени расплывается — ширина его увеличивается. Если дисперсия невелика, расплывание пакета происходит не слишком быстро. В этом случае пакету можно приписать скорость u, под которой понимается скорость, с которой перемещается центр пакета, т. е. точка с максимальным значением Е. Эту скорость называют групповой скоростью. В диспергирующей среде групповая скорость и отличается от фазовой скорости u (имеется в виду фазовая скорость гармонической составляющей с максимальной амплитудой, иными словами — фазовая скорость для доминирующей частоты). Ниже мы покажем, что в случае, когда dn/dl<0 групповая скорость оказывается меньше фазовой (u <u); в случае, когда dn/dlo>0, групповая скорость больше фазовой ((u >u)).

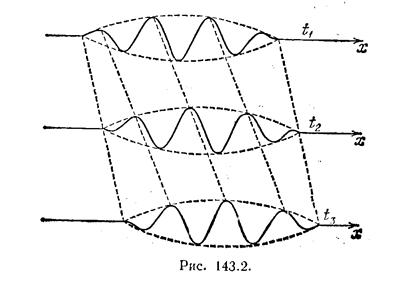
На рис. 143.2 показаны «фотографии» волнового пакета для трех последовательных моментов времени t₁, t₂ и t₃. Рисунок выполнен для случая, когда u<u. Из рисунка видно, что наряду с перемещением пакета происходит движение «горбов» и «впадин» «внутри» пакета, причем у левой границы пакета все время зарождаются новые «горбы», которые, пробежав вдоль пакета, исчезают у его правой границы. В результате, в то время как пакет в целом перемещается со скоростью u отдельные «горбы» и «впадины» перемещаются со скоростью u.

В случае, когда u>u направления перемещения пакета и движения «горбов» внутри него оказываются противоположными. Поясним сказанное на примере суперпозиции двух плоских волн с одинаковой амплитудой и разными длинами волн l.

На рис. 143.3 дана «моментальная фотография» волн. Одна из них изображена сплошной линией, другая — пунктирной. Интенсивность максимальна в точке А, где фазы обеих волн в данный момент совпадают. В точках B и С обе волны находятся в противофазе, вследствие чего интенсивность результирующей волны равна нулю. Допустим, что обе волны распространяются слева направо, причем скорость «сплошной» волны меньше, чем «пунктирной» (в этом случае 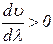, следовательно,

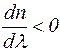Тогда место, в котором волны усиливают друг друга, будет со временем перемещаться влево относительно волн. В результате групповая скорость окажется меньше фазовой. Если скорость «сплошной» волны больше, чем «пунктирной» (т. е. dn/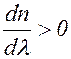место, в котором происходит усиление волн, будет перемещаться вправо, так что групповая скорость окажется больше фазовой.

Напишем уравнения волн, положив для упрощения формул начальные фазы равными нулю:

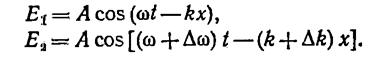
Здесь 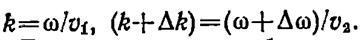,Пусть 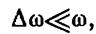соответственно 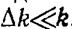Тогда, сложив колебания и произведя преобразования по формуле для суммы косинусов, получим

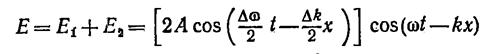(13.10)

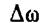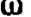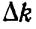(во втором множителе мы пренебрегли по сравнению с и по сравнению с k).

Множитель, стоящий в квадратных скобках, изменяется с х и t гораздо медленнее, чем второй множитель. Поэтому выражение (13.10) можно рассматривать как уравнение плоской волны, амплитуда которой изменяется по закону

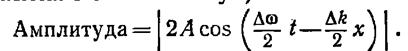
В данном случае имеется ряд одинаковых максимумов амплитуды, определяемых условием

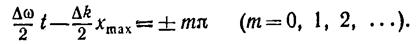(13.11)

Каждый из этих максимумов можно рассматривать как центр соответствующей группы волн.

Разрешив (13.11) относительно х_max получим

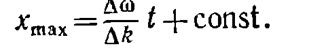
Отсюда следует, что максимумы перемещаются со скоростью

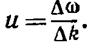
Полученное выражение представляет собой групповую скорость для случая, когда группа образована двумя составляющими.

Групповой пакет неизбежно деформируется. Если эта деформация осуществляется медленно, то полученные закономерности приближенно выполняются. Более точная формулировка условий существования недеформируемой группы волн предполагает наличие узкого спектра синусоидальных волн, образующих группу, и определенных свойств среды, в которой происходит ее распространение [отсутствие резких изменений n(l) вблизи l₀]. При нарушении этих условий импульс быстро деформируется («расползается») и описание движения его как целого становится неточным.

Итак, групповая скорость 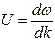, тогда как фазовая скорость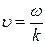

Найдем связь между фазовой и групповой скоростями,

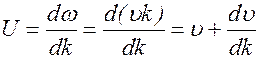
Это выражение легко преобразовать, учитывая, что

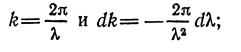
тогда окончательно получается выражение, называемое формулой

Рэлея:

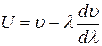
Проведем подробный анализ найденного соотношения между фазовой и групповой |скоростями.

1. Если 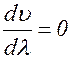т. n = const, то дисперсия отсутствует и 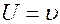иными словами, фазовая и групповая скорости совпадают. Это справедливо не только для вакуума, но и для некоторых материальных сред. В частности, для световых волн в воздухе и воде можно не учитывать дисперсии, так как она пренебрежимо мала

2. Если 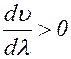., то 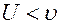. Этот случай, как правило, реализуется при прохождении света через различные стекла и другие прозрачные среды. Заметим, что если 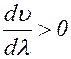, то 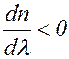, то так как

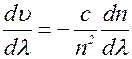
Следовательно, показатель преломления n уменьшается с увеличением длины волны. Эту часто встречающуюся зависимость n от l называют нормальной дисперсией.

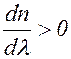3. Если , то U> u. В этом случае , т. е. показатель преломления возрастает с увеличением длины волны. В дальнейшем будет показано, что такая зависимость n от l может иметь место в тех областях спектра, где наблюдается интенсивное поглощение света. Она называется аномальной дисперсией.

Заключение

Необходимо помнить, что вид поляризации зависит от разности фаз, колебаний взаимодействующих световых векторов. По Френелю линейно поляризованный свет можно представить как совокупность двух волн, имеющих правую и левую круговую поляризацию. Скорость распространения этих волн в средах, имеющих ассиметричные молекулы, различна, поэтому между этими волнами возникнет разность фаз. Чтобы результирующая волна по-прежнему оставалась линейно поляризованной, необходимо чтобы результирующий вектор напряженности электрического поля испытал поворот относительно своего первоначального положения. Поворот плоскости поляризации в оптических средах дает возможность исследовать структурную формулу вещества, измерять концентрацию оптически активных веществ в растворе. С помощью поляризованного света изучают структуру и свойства различных веществ, причем в ряде случаев эти методы оказываются значительно чувствительнее методов рентгеноструктурного анализа. С помощью поляризованного света исследуют межмолекулярные взаимодействия, в частности перенос энергии возбуждения между молекулами в растворах и кристаллах. Биохимики определяют детали структуры белков, аминокислот и отдельных элементов клетки.

Ст. преподаватель кафедры___________________________

(наименование кафедры)

_______________________ ________________________

(ученая степень, ученое звание, подпись) (И.О.Ф.)

«____»________________г.

Дата добавления: 2014-01-14