Й учебный вопрос. Методы оценивания параметров структурных моделей

Матрица коэффициентов (3)

Матрица коэффициентов (2)

Матрица коэффициентов (1)

Уравнение	Переменные
х3	х4
	а23 0	а24 0

Следовательно, достаточное условие идентификации не выполняется и первое уравнение нельзя считать идентифици­руемым.

Для второго уравнения Н = 2 (у₁, у₂), D = 1 (отсутствует х₁) счетное правило дает утвердительный ответ: уравнение иденти­фицируемо D + 1 = Н.

Достаточное условие идентификации выполняется. Коэффи­циенты при отсутствующих во втором уравнении переменных со­ставят.

Уравнение	Переменные
у3	х1
	b23 -1	а11 a31

Согласно таблице определитель матрицы равен 0, а ранг матрицы равен 2, что соот­ветствует следующему критерию: ранг матрицы коэффициентов должен быть не меньше числа эндогенных переменных в системе без одной. Итак, второе уравнение точно идентифицируемо.

Третье уравнение системы содержит Н = 3 и D = 2, т. е. по не­обходимому условию идентификации оно точно идентифицируе­мо (D + 1 = Н). Противоположный вывод имеем, проверив уравнение на достаточное условие идентификации. Составим таблицу коэффициентов при переменных, отсутствующих в тре­тьем уравнении, в которой определитель матрицы равен нулю.

Уравнение	Переменные
х3	х4
	0 a23	0 a24

Из таблицы видно, что достаточное условие идентификации не выполняется. Уравнение неидентифицируемо. Следовательно, рассматриваемая в целом структурная модель, идентифицируе­мая по счетному правилу, не может считаться идентифицируемой исходя из достаточного условия идентификации.

Коэффициенты структурной модели могут быть оценены раз­ными способами в зависимости от вида системы. Наибольшее распространение в литературе получили следующие методы оценивания коэффициентов структурной модели:

· косвенный метод наименьших квадратов (КМНК);

· двухшаговый метод наименьших квадратов (ДМНК);

· трехшаговый метод наименьших квадратов (ТМНК);

· метод максимального правдоподобия с полной информа­цией (ММП f);

· метод максимального правдоподобия при ограниченной
информации (ММП s).

Косвенный и двухшаговый методы наименьших квадратов подробно описаны в литературе и рассматриваются как традици­онные методы оценки коэффициентов структурной модели. Эти методы достаточно легкореализуемы. Косвенный метод наи­меньших квадратов применяется для идентифицируемой систе­мы одновременных уравнений, а двухшаговый метод наимень­ших квадратов — для оценки коэффициентов сверхидентифииируемой модели.

Метод максимального правдоподобия рассматривается как наиболее общий метод оценивания, результаты которого при нормальном распределении признаков совпадают с МНК. Одна­ко при большом числе уравнений системы этот метод приводит к достаточно сложным вычислительным процедурам. Поэтому в качестве модификации используется метод максимального прав­доподобия при ограниченной информации (метод наименьшего дисперсионного отношения), разработанный в 1949 г. Т. Андерсо­ном и Н. Рубиным.

В отличие от метода максимального правдоподобия в данном методе сняты ограничения на параметры, связанные с функцио­нированием системы в целом. Это делает решение более про­стым, но трудоемкость вычислений остается достаточно высо­кой. Несмотря на его популярность, к середине 1960-х годов он был практически вытеснен двухшаговым методом наименьших квадратов в связи с гораздо большей простотой последнего.

Дальнейшим развитием двухшагового метода наименьших квадратов является трехшаговый МНК (ТМНК), предложенный в 1962 г. А. Зельнером и Г. Тейлом. Этот метод оценивания приго­ден для всех видов уравнений структурной модели. Однако при некоторых ограничениях на параметры более эффективным ока­зывается ДМНК.

Как уже отмечалось, косвенный метод наименьших квадра­тов используется в случае точно идентифицируемой структурной модели. Процедура применения КМНК предполагает выполне­ние следующих этапов работы:

· структурная модель преобразовывается в приведенную фор­му модели;

· для каждого уравнения приведенной формы модели обыч­ным МНК оцениваются приведенные коэффициенты ();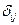

· коэффициенты приведенной формы модели трансформиру­ются в параметры структурной модели.

Если система сверхидентифицируема, то КМНК не использу­ется, ибо он не дает однозначных оценок для параметров струк­турной модели. В этом случае могут применяться разные методы оценивания, среди которых наиболее распространенным и про­стым является двухшаговый метод наименьших квадратов.

Основная идея ДМНК — на основе приведенной формы мо­дели получить для сверхидентифицируемого уравнения теорети­ческие значения эндогенных переменных, содержащихся в пра­вой части уравнения. Далее, подставив их вместо фактических значений, можно применить обычный МНК к структурной фор­ме сверхидентифицируемого уравнения. Метод получил назва­ние «двухшаговый метод наименьших квадратов», ибо МНК ис­пользуется дважды: на первом шаге при определении приведенной формы модели и нахождении на ее основе оценок теоретических значений эндогенной переменной и на втором шаге применительно к структурному сверхидентифицируемому уравнению при определении структурных коэф­фициентов модели по данным теоретических (расчетных) значе­ний эндогенных переменных.

Сверхидентифицируемая структурная модель может быть двух типов:

· все уравнения системы сверхидентифицируемы;

· система содержит наряду со сверхидентифицируемыми точ­но идентифицируемые уравнения.

Если все уравнения системы сверхидентифицируемые, то для оценки структурных коэффициентов каждого уравнения исполь­зуется ДМНК. Если в системе есть точно идентифицируемые уравнения, то структурные коэффициенты по ним находятся из системы приведенных уравнений.

Заключение — до 5 мин.

Несмотря на важность системы эконометрических уравнений, на практике часто не принимают во внимание некоторые взаимосвязи. Ее использование сопряжено с рядом сложностей, которые связаны с ошибками спецификации модели. Ввиду большого числа факторов, влияющих на экономические переменные, исследователь, как правило, не уверен в точности предлагаемой модели. Набор эндогенных и экзогенных переменных модели соответствует теоретическому представлению исследователя о моделируемой объекте, которое сложилось в конкретный момент времени и может позднее изменится.

Содержание и методические рекомендации:

- обобщить наиболее важные, существенные вопросы лекции.

- сформулировать общие выводы.

- поставить задачи для самостоятельной работы.

- ответить на вопросы студентов.

Дата добавления: 2014-01-14