
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Индекс себестоимости
|
|
|
|
В качестве примера рассмотрим индекс себестоимости.
Предположим, что определенный вид продукции производится на нескольких предприятиях. Если обозначить себестоимость единицы продукции через с (раньше обозначали через х), а выпуск продукции отдельных предприятий как веса через q (раньше – f), можно записать формулы индексов себестоимости.
Индекс себестоимости переменного состава:
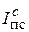 =
=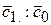 =
= 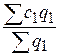 :
: 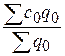 . (25)
. (25)
Индекс себестоимости фиксированного состава:
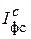 =
= 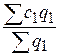 :
: 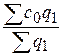 , т.е. (25,а)
, т.е. (25,а)
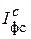 =
= 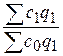 . (25,б)
. (25,б)
Индекс структурных сдвигов себестоимости:
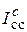 =
= 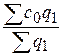 :
: 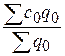 . (26)
. (26)
Пример. Имеются данные о выпуске и себестоимости одноименного продукта по трем предприятиям (табл. 4). Требуется определить изменение себестоимости единицы продукции на каждом предприятии, а также в целом по всем предприятиям с помощью индексов: а) переменного состава, б) фиксированного состава, в) структурных сдвигов.
Таблица 11.4
| Номер предприятия | Базисный период | Отчетный период | ||||
| Выпуск продукции | Себестоимость единицы продукции, руб.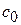
| Выпуск продукции | Себестоимость единицы продукции, руб.
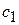
| |||
тыс.
единиц
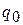
| в долях к итогу
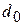
| тыс. единиц
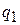
| в долях к итогу
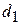
| |||
| 0,50 | 0,40 | 14,2 | ||||
| 0,30 | 0,28 | 12,5 | ||||
| 0,20 | 0,32 | 9,5 | ||||
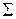
| 1,00 | (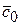 =13,4) =13,4)
| 1,00 | (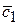 =12,22) =12,22)
|
1) Расчет индивидуальных индексов себестоимости продукции по каждому предприятию дает следующие результаты:
По 1-му предприятию 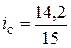 = 0,947 (или 94,7%);
= 0,947 (или 94,7%);
По 2-му предприятию 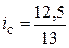 = 0,961 (или 96,1%);
= 0,961 (или 96,1%);
По 3-му предприятию 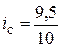 = 0,95 (или 95%);
= 0,95 (или 95%);
2) Для расчета индекса себестоимости переменного состава рассчитаем:
а) среднюю себестоимость в базисном периоде:
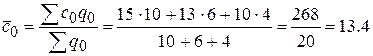 руб.;
руб.;
а) среднюю себестоимость в отчетном периоде:
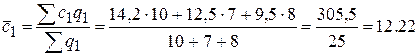 руб.,
руб.,
тогда по формуле (11.23)
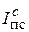 =
=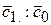 , т.о.
, т.о. 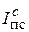 =
=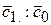 = 12,22: 13,4 = 0,912 (или 91,2%),
= 12,22: 13,4 = 0,912 (или 91,2%),
т.е. средняя себестоимость единицы продукции снизилась на 8,8%.
Пояснения.
· Если бы продукции по отдельным предприятиям оставался без изменения или изменился всюду пропорционально, т.е. если удельный вес каждого предприятия в выпуске продукции оставался неизменным, то тогда, очевидно, снижение средней себестоимости на 8,8% можно было бы объяснить только снижением себестоимости на каждом предприятии. Фактически же в рассматриваемом примере менялась не только себестоимость на каждом предприятии, но и удельный вес каждого предприятия в общем выпуске продукции. Следовательно, снижение средней себестоимости на 8,8% достигнуто за счет изменения двух факторов (с и q ).
· В примере общий индекс переменного состава меньше, чем каждый из индивидуальных индексов, т.е. снижение средней себестоимости (8,8%) оказалось больше, чем снижение себестоимости на отдельных предприятиях (5,3: 3,9 и 5%), Очевидно, что это можно объяснить изменением структуры выпуска, в частности увеличением доли 3-го предприятия, имеющего самую низкую себестоимость.
3) Чтобы исключить влияние изменения структуры совокупности на динамику средних величин, рассчитаем индекс себестоимости фиксированного состава по формуле (25,а) (приняв в качестве фиксированной структуру выпуска отчетного периода 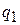 ):
):
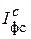 =
= 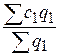 :
: 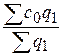 = 1,22:
= 1,22: 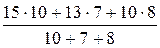 = = 1,22: 1,84 – 0,952 (или 95,2%).
= = 1,22: 1,84 – 0,952 (или 95,2%).
Пояснение.
· 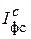 , характеризуя среднее изменение себестоимости на всех трех предприятиях, не может выходить за пределы значений
, характеризуя среднее изменение себестоимости на всех трех предприятиях, не может выходить за пределы значений 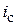 (см. замечание 3), т.е для данного примера не может быть меньше 94,1% и не может быть больше 96,1%, что и подтверждается.
(см. замечание 3), т.е для данного примера не может быть меньше 94,1% и не может быть больше 96,1%, что и подтверждается.
(Вычислите 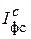 по (25,б) и сопоставьте результаты.)
по (25,б) и сопоставьте результаты.)
4) Влияние структурного фактора отразим с помощью индекса структурных сдвигов (см. 26):
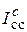 =
= 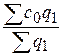 :
: 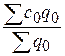 = 12,8: 13,4 = 0,958 = 0,958 (или 98,8%).
= 12,8: 13,4 = 0,958 = 0,958 (или 98,8%).
Пояснение.
· Данный результат означает, что на 4,2% (95,8-100) средняя себестоимость снизилась за счет структурного фактора, в частности, за счет увеличения доли продукции на 3-м предприятии с более низкой себестоимостью и за счет уменьшения доли выпуска на 1-м предприятии с более высокой себестоимостью.
(Вычислите 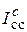 по (24) и сопоставьте результаты.)
по (24) и сопоставьте результаты.)
5) Значения 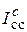 ,
, 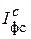 и
и 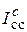 можно получить, используя в качестве весов доли по предприятиям d (см. графы 3 и 6 в табл. 4) вместо q, т.е.
можно получить, используя в качестве весов доли по предприятиям d (см. графы 3 и 6 в табл. 4) вместо q, т.е.
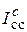 =
= 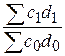 ;
; 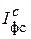 =
= 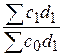 ;
; 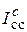 =
= 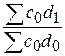 .
.
Вычислите по этим формулам 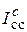 ,
, 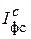
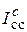 и сопоставьте результаты.
и сопоставьте результаты.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 1395; Нарушение авторских прав?; Мы поможем в написании вашей работы!