Метод Рунге-Кутта второго порядка

Семейство методов Рунге-Кутта второго порядка имеет вид:

x_i+1 = x_i + h{(1-а) f(t_i , x_i) +af(t_{i +} }_, i = 0, 1, 2,…, n.

При а = 1 получаем модифицированный метод Эйлера.

Рассмотренные методы Рунге-Кутта относятся к классу одношаговых методов, в которых для вычисления значения очередной точке x_k+1 нужно знать значение в предыдущей точке x_k. Ещё один класс решения задачи Коши - многошаговые методы, в которых используются точки x_k-3, x_k-2, x_k-1, x_k для вычисления x_k+1. В многошаговых

методах первые четыре начальные точки (t₀ , x₀), (t_i, x_i), (t₂ , x₂) (t₃ , x₃) должны быть получены заранее любым из одношаговых методов. Наиболее известным многошаговым методом является метод прогноза-коррекции Адамса.

Для решения дифференциальных уравнений и систем в Matlab предусмотрены следующие фунукции:

ode45(f, interval, x0);

ode23(f, interval, x0);

ode113(f, interval, x0);

ode15s(f, interval, x0);

ode23s(f, interval, x0);

ode23t(f, interval, x0);

ode23tb(f, interval, x0).

Входными параметрами этих функций являются:

f - вектор-функция для вычисления правой части уравнения или системы уравнений;

interval – массив из двух чисел, определяющий интервал интегрирования уравнения или системы уравнений;

x0 – вектор начальных условий.

В функции ode45 реализован метод Рунге-Кутта 4-5 порядка точности, в функции ode23 также реализован метод Рунге-Кутта, но 2-3 порядка, а функция ode113 реализует метод Адамса.

Пример:

Решить задачу Коши:

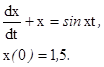
Чтобы дифференциальное уравнение вида 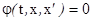можно было решить посредством функций Matlab, его необходимо преобразовать к виду y =F(t, x) и записать в виде М-файла (рис. 1)

Рис. 1.

В рабочем окне программы Matlab записывается команда, атрибуты которой содержат имя функции, интервал интегрирования, начальные условия (рис. 2).

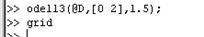
. Рис. 2.

Результаты решения представлены на рис. 3.

С Рис. 3.

Пример 2. Рассмотрим решение системы уравнений

, y₁(0) = 0, y₂(0) = 0,

на интервале [0;10].

М – файл и команды в рабочем окне (рис. 4)

Рис. 4.

Результат решения представлен на рис. 5.

Рис. 5.

Дата добавления: 2014-01-14