Основной недостаток ИВС в том, что это сигналы с пассивной паузой

Сомкнутые ортогональные в точке составные сигналы (СОТС)

Это второй класс составных сигналов.

Сомкнутые – означает, что это сигналы без пассивной паузы.

Ортогональные в точке – означает, что это сигналы, которые ортогональны только при одном временном сдвиге друг относительно друга, т.е. коэффициент взаимной корреляции равен нулю только при одном временном сдвиге. Имеется временной сдвиг равный нулю. Тогда, когда время их существования совпадает.

СОТС также представляются матрицей строкой.

Количество временных сигналов не произвольно: К кратно двум.

Сомкнутые сигналы – все К временных позиций заняты.

Для того, чтобы создать множество сигналов необходимо использовать фазовые различия.

Поэтому при построении такого рода сигналов используют радиоимпульсы с двумя значениями фазы 0 и π радиан.

Условно импульс с фазой 0 будем обозначать "1", с фазой π – "-1".

Тогда множество СОТС удобно представлять с помощью матрицы Адамара.

Матрица Адамара – матричная конструкция, позволяющая рекуррентное увеличение размерности.

Матрица Адамара первого порядка имеет следующий вид:

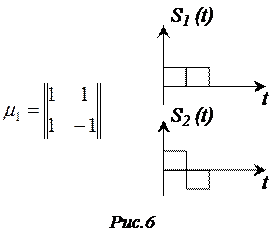Столбцы и строки это матрицы представляют два СОТС сигнала.

Матрица Адамара порядка μ _j+1 формируется из четырёх матриц предшествующего порядка.

Все эти сигналы ортогональны.

В радио форме это будут радиоимпульсы с фазой, отличающийся на π радиан от радиоимпульсов, которые заменяют положительные импульсы.

Эта система функций называется Функция Радемахера-Уолша.

В функции Радемахера-Уолша принято следующее обозначение

F(Т, 0)

Т – длительность сигнала, 0 – означает, что на длительности сигнала не было ни одного перехода.

F(Т, 3) – три перехода.

При таком обозначении функции Радемахера-Уолша обладают следующим свойством:

При осуществлении двоичного умножения (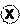) двух функций F(Т, i) и F(Т, j), получим функцию того же вида F(Т,i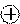j)

Это свойство упрощает генерацию множества таких функций.

Если мы сгенерируем какое-то ограниченное множество базовых функций, то все остальные могут быть получены путём перемножения этих функций.

Т.е. генератор генерирует базовое количество функций, а потом путём взаимного перемножения получаются остальные функции.

В данном случае проще всего сгенерировать функцию F(Т, 3) – мультивибратором.

Из функции F(Т, 3) путём триггерного деления можно получить F(Т, 1).

Вначале генерируются функции, которые проще всего сгенерировать.

Домашнее задание:

Построить генератор множества функций Радемахера-Уолша для матрицы третьего порядка μ ₃.

Это будет восемь функций.

Переход к радиосигналам: нужно промодулировать этими функциями по фазе гармонический сигнал с изменением в фазе на π радиан.

Эти СОТС сигналы по своим свойствам лучше, чем ИВС:

1. В частотно временной области таких сигналов можно построить гораздо больше
2. Такие сигналы – сигналы с активной паузой, т.е. они гораздо более помехоустойчивые

Шумоподобные (Псевдошумовые) сигналы ПШС.

Третья категория сигналов.

Также представляются матрицей строкой.

Количество временных позиций К не произвольное.

Шумоподобные сигналы имеют огибающую в виде т.н. последовательности максимальной длины регистра сдвига ("m"-последовательностей).

Эти последовательности генерируются генератором, построенным на регистре сдвига с обратными связями или сумматорами по модулю 2.

Функциональная схема простейшего генератора "m"-последовательностей, построенного на регистре сдвига из трёх ячеек.

Регистр сдвига – цепочка триггеров, управляемая генератором тактовых импульсов (ГТИ).

ГТИ с каким-то тактом τ с и м вола осуществляет перемещение по регистру сдвига.

Для того чтобы генератор работал, необходима обратная связь.

Чтобы генератор работал первоначально, в регистр сдвига нужно что-то записать (1 0 0).

Когда поступает первый тактовый импульс "1" перемещается в следующую ячейку, на выход поступил "0", на вход сумматора по модулю два поступило "0" и "0".

В следующем такте запись будет 0 1 0.

Далее 1 0 1.

В третьем такте 1 1 0:

Через какое-то количество тактов последовательность, которая получается на выходе, будет повторяться. Количество тактов, через которое последовательность на выходе повторяется, называется периодом последовательности.

В зависимости от того, как организовать обратную связь, период последовательности будет различным.

Та последовательность, которая будет иметь наибольший период, называется последовательностью максимальной длины этого регистра сдвига.

Эта длина и есть 2^r-1, где r – количество ячеек в регистре сдвига.

Если регистр сдвига достаточно большой длины, то вариантов обратной связи, при котором получается М-последовательность, может быть несколько. Но всегда, не зависимо от того, сколько будет вариантов, максимальный период последовательности будет 2^r-1.

Для того чтобы из М-последовательности получить ПШС нужно М-последовательностью промодулировать по фазе гармонический сигнал с изменением фазы на π радиан.

Вид автокорреляционной функции М-последовательности:

		Рис.11

Т_ТКС – длительность шумового сигнала или временной интервал, выделенный телекоммуникационной системой.

Если r → ∞ (при сохранении длительности) R(τ) → дельта функция в нуле.

Дельта функция – корреляционная функция белого шума.

Вот почему такие сигналы называют псевдошумовые.

В пределе при r → ∞ свойства таких сигналов стремятся к свойствам белого шума.

ПШС являются симплексными сигналами, т.е. обладают минимальным уровнем взаимной корреляции

(1)

ПШС являются также сигналами с активной паузой – нет интервалов между импульсами.

Домашнее задание:

Построить согласованный фильтр для ПШС. Схема согласованного фильтра для ПШС. Или приёмник для множества таких сигналов.

Частотно временные сигналы (ЧВС).

Четвёртый тип сигналов.

ЧВС представляются полной матрицей (на прошлой лекции рисовали).

Чтобы ЧВС были ортогональными необходимо, чтобы ни в одной паре сигналов на одной и той же временной позиции не было радиоимпульса одной и той же частоты.

Если это условие выполняется и если сами радиоимпульсы матрицы ортогональны, то тогда ЧВС будут ортогональны.

Телекоммуникационные системы с различными методами уплотнения/разделения каналов.

(изучаем Линейные методы уплотнения каналов с закреплёнными каналами.)

Системы с временным уплотнением и разделением каналов

Временное уплотнение/разделение каналов означает, что ортогональность обеспечивается разделением сигналов по времени.

Упрощённая функциональная схема телекоммуникационной системы с временным уплотнением каналов

Передающая часть:

Первичные сигналы поступают на вход коммутатора передатчика – К₁. В коммутатор может также поступать кадровый синхросигнал.

Выход коммутатора подключается к аналогово-цифровому преобразователю (АЦП).

Приёмная часть:

В коммутатор приёмника – К₂

Коммутатор приёмника К₁ с постоянным периодом Т_К подключает выход каждого из ЭФП к АЦП.

Причём каждый из ЭФП подключается к АЦП на время Т _{СЛ ОВА}.

Что делает коммутатор с каждым первичным сигналом?

Коммутатор осуществляет временную дискретизацию всех первичных сигналов с постоянным периодом Т_{Коммутации}. При этом каждый первичный сигнал подключается на некий постоянный интервал Т _{СЛ ОВА}.

Какова ещё одна функция коммутатора?

Функция временного уплотнения каналов.

В АЦП значение * превращается в цифровую форму – формируется кодовое слово.

АЦП выполняет функцию квантования по уровню и словную синхронизацию.

В приёмной части коммутатор осуществляет временное разделение каналов.

На выходе коммутатора получаем дискретное значение первичного сигнала, а нужно восстановить сам первичный сигнал. Вторая функция декодера источника – из дискретных значений первичного сигнала формирование непрерывного первичного сигнала – выполняется, если это необходимо, в преобразователе в нужную форму (ПНФ).

Для того чтобы временное разделение каналов было выполнено корректно, т.е. чтобы дискретные значения первичного сигнала соответствующего источника попали к соответствующему потребителю необходимо, чтобы коммутаторы приёмника и передатчика работали синхронно и синфазно. Это обозначает, что когда на вход коммутатора приёмника К₁ поступает дискретное значение первичного сигнала i-го источника, выход коммутатора К₂ должен быть подключён к каналу i-го потребителя. Синхронность и синфазность обеспечивается кадровой и словной синхронизацией. Кадровая обеспечивает синхронность и синфазность по подключению, а словная – синфазность по длительности подключения кодового слова.

Словная синхронизация используется и в ЦАП, и в ДКК.

Как выбрать период коммутации?

Период коммутации выбирают, исходя из самого быстрого источника – максимальной частоты в спектре первичных сигналов.

Тогда все остальные источники (медленнее) будут слишком часто передавать – будет возникать методическая или конструктивная избыточность.

Чем медленнее источник, тем с большей избыточностью он будет передавать.

Домашнее задание:

Дата добавления: 2014-01-14