Слайд 76. К понятию робастной системы с эталонной моделью

На первом этапе (процедура идентификации) (см. слайд 76). функционирования алгоритма решается оптимизационная задача:

,

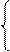
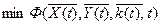
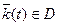где 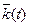– вектор дрейфующих параметров эталонной модели, подлежащих идентификации; – функционал невязки между экспериментальными и рассчитанными по эталонной модели значениями выходных параметров;–область допустимых решений (выбирается из априорных знаний об объекте управления). Текущая информация, в таких алгоритмах управления, используется для идентификации неизвестных параметров, заложенных в математическую модель как неизвестные константы. Как правило, метод идентификации, при этом, относится к классу задач квадратического программирования (например, метод наименьших квадратов).

На втором шаге (процедура оптимизации) (см. слайд 76) априорная информация формализована в виде математической модели и используется для отыскания оптимального режима и принятия решения по управлению процессом (см. слайд 76). При этом решается оптимизационная задача вида:

,

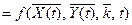
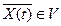где 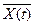– оптимальные значения управляющих параметров; 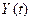– эталонная математическая модель объекта управления; V- область допустимых значений управляющего воздействия.

Метод оптимизации, при этом, выбирается с учётом особенностей критерия управления (эталонной модели объекта):

-если критерий управления линейная функция, то применяются методы линейного программирования (Например, симплекс-метод);

-если критерий управления нелинейная функция, то применяются методы нелинейного программирования (Например, метод Гаусса-Зейделя);

-если критерий управления – это траектория движения, то применяются методы динамического программирования (Например, принцип максимума Понтрягина);

-если применяются интегральные критерии качества, то применяются методы квадратического программирования (Например, Метод наименьших квадратов);

-если применяются обобщенные критерии качества, измерение которых возможно лишь косвенными методами, то применяются методы стохастического программирования.

Основной особенностью при проектировании робастных систем является согласование темпов обработки измерительной информации в информационной и управляющей подсистемах. Если обозначить время работы процедуры идентификации как: 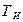, а время работы процедуры оптимизации как: 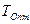, то суммарное время обработки информации должно быть меньше периода нанесения управляющего воздействия, :

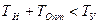
Кроме того, при проектировании робастных систем с эталонной моделью необходимо учитывать, что:

1. Достоверность принятого решения зависит не столько от точности и чувствительности применяемых технических средств измерения, сколько от сложности эталонной модели объекта управления; поэтому на первый план выдвигаются вопросы выбора и обоснования метода программирования, который зависит от вида эталонной модели;

2. Разработка алгоритмов визуализации процессов измерения и управления многократно усложняется; Уже не достаточно обходится визуализацией рабочей точки. Необходимо отображать процесс адаптации.

3. проблемой является количественно обоснованный выбор эталонной модели, удовлетворяющей условию.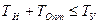

Пример 11.2. Адаптивное управление температурным профилем ректификационной колонны тарельчатого типа. (см. слайд 81). Поставлена задача, повысить качество продукции путем изменения температурного профиля по высоте колонны. Основным управляющим параметром является температура на тарелке питания, Y₅(t), которая изменяется при помощи расхода теплоносителя, X₁(t).

Качество целевого продукта достигается при помощи прогноза температуры тарелки питания по эталонной математической модели температурного профиля Y_i, по высоте колонны:

.

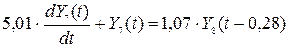
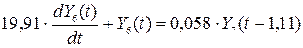
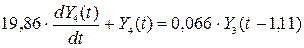
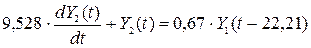
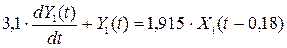При этом, критерий эффективности работы ректификационной колонны функционирует по алгоритму:

,

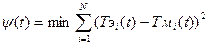где: N – количество датчиков температуры, установленных по высоте колонны; Тэ_i(t) – текущее значение температуры i-той тарелки, измеренное на объекте управления; Тм_i(t) – текущее значение температуры i-той тарелки, прогнозируемое по математической модели ректификационной колонны.

Модели измерительной информации были получены методом статистического моделирования по методике из работы [44], а их адекватность проверялась по критериям Фишера и Стьюдента.

Устройство состоит из колонны 1, блока датчиков температур 2, теплообменников (блоки 3 и 13), промышленных хроматографов (блоки 4 и 9), главного (блок 5) и вспомогательного (блок 6) регуляторов температуры куба, блока стабилизации нижней части температурного профиля колонны 7, дефлегматора (блок 8), главного (блок 10) и вспомогательного (блок 11) регуляторов температуры верха, блока стабилизации верхней части температурного профиля колонны 12, блока идентификации текущего значения эффективности работы ректификационной колонны 14, главного (блок 15) и вспомогательного (блок 16) регуляторов температуры питательной смеси.

Устройство функционирует следующим образом. Информация, генерируемая датчиками температур 2, постоянно попадает в регулятор температуры куба 5, регулятор температуры верха 10 и в блок 14, в котором производится накопление текущих реализаций, идентификация настроечных коэффициентов математической модели ректификационной колонны и строится модельный профиль температур по высоте колонны.

Температурный профиль по высоте колонны фиксируется тремя управляющими воздействиями: расход перегретого пара, поступающего в теплообменник 3, расход хладагента, подаваемого в дефлегматор 8, и температура тарелки питания, которую можно изменять с помощью теплообменника 13. При этом два из управляющих воздействий (расход перегретого пара и расход хладагента) определяют начальное (температура куба) и конечное (температура верха колонны) значения профиля температур по высоте колонны.

На протяжении всего периода идентификации должны быть зафиксированы температура куба посредством блока 5, температура верха колонны посредством блока 10 и температура тарелки питания посредством блока 15.

В каскадной системе регулирования температуры куба (блок 7), выходная величина промышленного хроматографа 4 поступает в качестве задания на регулятор температуры куба 5, вырабатывающий задание регулятору 6, предназначенному для стабилизации расхода перегретого пара, поступающего в теплообменник 3.

Слайд 81. К понятию робастной системы с эталонной моделью

Аналогично в каскадной системе регулирования температуры верха (блок 12), выходная величина промышленного хроматографа 9 поступает в качестве задания на регулятор температуры верха 10, который вырабатывает задание регулятору 11, предназначенному для стабилизации расхода хладагента, поступающего в дефлегматор 8.

Блок идентификации текущего значения эффективности работы ректификационной колонны 14, кроме идентификации математической модели и вычисления модельного профиля температур 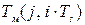, вычисляет также минимальное значение квадрата отклонении модельного профиля температур по высоте колонны от измеренного температурного профиля 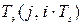. Минимум ищется по математической модели ректификационной колонны, представленной в главе 2, методом градиентного поиска по температуре питающей тарелки. Величина минимума принимается за текущее значение эффективности работы ректификационной колонны и устанавливается в качестве задания регулятору температуры питающей смеси 15. Само же изменение текущего значения температуры питающей смеси осуществляется путем изменения расхода греющего пара посредством теплообменника 13 регулятором 16.

Дата добавления: 2014-01-14