
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Теория подобия процессов переноса
|
|
|
|
 =-
=-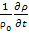 ; С ростом температуры плотность уменьшается.
; С ростом температуры плотность уменьшается.
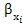 =-
=-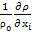 ; С ростом
; С ростом 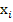 плотность уменьшается (
плотность уменьшается (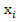 - концентрация компонента меньшей плотности).
- концентрация компонента меньшей плотности).
dρ=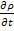 dt+
dt+ =
=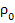 +
+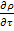 △t+
△t+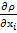 △
△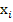 =
=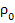 -
-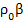 *△t-
*△t-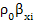 △
△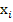
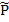 =P+ρgz – приведенное давление
=P+ρgz – приведенное давление
 ρ[
ρ[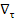 ω+ω
ω+ω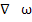 ]=-∇P-ρg+µ
]=-∇P-ρg+µ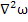 =-∇
=-∇ 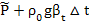 +
+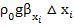 + µ
+ µ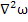
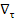 t+ω
t+ω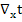 =- a
=- a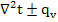 /Сρ
/Сρ
 +ω
+ω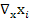 =-
=- 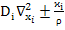
α[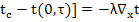
β[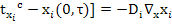
Система уравнений переноса количества движения, тепла и вещества с граничными условиями 3 рода.
Введем безразмерные параметры:
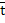 =
=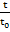 ;
;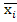 =
=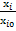 ;
;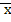 =
= ;θ=
;θ=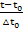
φ= ; Re=
; Re=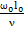 ; Pe=
; Pe=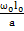 ;
;  =
=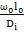
Pr= ;
;  =
=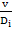 ; Le=
; Le=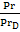 =
=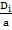 - критерий Льюиса.
- критерий Льюиса.
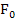 =
= ;
; =
= ;
;
Gr= ;
; 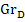 =
=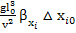 ;
;
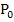 =
=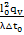 ;
;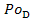 =
=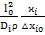
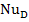 =
= ; Nu=
; Nu=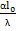
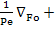 ω
ω =-∇
=-∇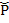 +
+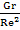 θ+
θ+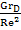 φ+
φ+
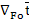 +Pe
+Pe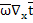 =-
=-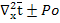
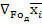 +
+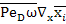 =-
=-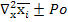 D
D
Nu[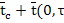 )]=-∇
)]=-∇
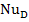 [
[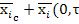 )]=-∇
)]=-∇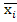
Nu,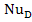 =f(Fo,
=f(Fo,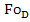 ,Re,Pr,
,Re,Pr,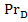 ,Gr,
,Gr, Po,
Po,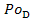 ) в случае независимого переноса тепла и вещества имеем:
) в случае независимого переноса тепла и вещества имеем:
Nu= f(Fo, Re, Pr, Gr,
Gr, Po
Po );
); 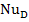 = f(
= f(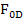 ,Re,
,Re,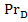 ,
,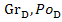 )
)
Аналогия между переносом тепла и массы (аналогия Льюиса)
Для стационарного конвективного переноса тепла и вещества имеем критериальные зависимости:
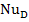 =
= =C
=C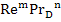 ;
;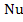 =
=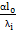 = C
= C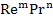 . Поделим выражения друг на друга:
. Поделим выражения друг на друга:
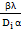 =
=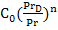 =
= =
= =>
=> =
= =
=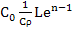 =
= .
.
Следовательно, зная α, можно рассчитать β и наоборот.
Основное уравнение гидродинамики (Навье-Стокса) для многокомпонентной среды.
В многокомпонентной среде возникает дополнительное изменение количества движения, связанное с диффундирующими потоками массы и источниками (стоками) за счет химического превращения:
 [
[ =
= +
+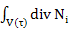 dV-
dV-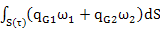 +
+ (
(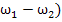 -
-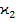 (
(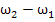 )]dV
)]dV
Σ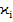 =0;
=0;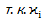 =-
=-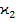 и (
и (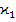 +
+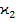 )(
)( -
- )=0
)=0
Σ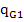 =0;
=0;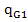 =-
=-
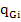 =
=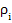 (
( =
=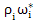
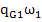 +
+ =
=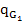 (
(
С учетом сделанных замечаний и выполненных ранее преобразований уравнение гидродинамики приводится к виду
ρ[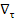 ω+ω
ω+ω ]=-∇P+ρ
]=-∇P+ρ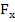 +∇[µ∇ω-
+∇[µ∇ω-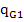 (
( ]
]
Последний член уравнения называют диффузионной вязкостью. Оценим его вклад:
A=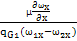 =
=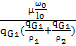 =
=
При больших 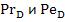 и малых
и малых  можно пренебречь диффузионной вязкостью.
можно пренебречь диффузионной вязкостью.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 448; Нарушение авторских прав?; Мы поможем в написании вашей работы!