
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Слайд 76 К понятию о комбинированных робастных системах
|
|
|
|
В комбинированных робастных системах процедура идентификации, которая предназначена для отслеживания дрейфа динамических характеристик эталонной модели объекта управления, реализуется только методами нелинейного программирования. При этом сложность модели такова, что не выполняется ограничение:  . и на оптимизацию времени не остается.
. и на оптимизацию времени не остается.
Тогда оптимальное значение управляющего воздействия можно найти, зная информацию о прошлом объекта управления и предназначенную для идентификации положения рабочей точки объекта управления на критерии управления. Это можно сделать по алгоритму:
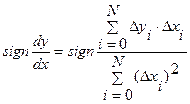 ,
,
где 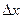 ,
, 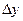 – флуктуация входных и выходных параметров объекта, полученные из хранимой в памяти ЭВМ прошлой информации;
– флуктуация входных и выходных параметров объекта, полученные из хранимой в памяти ЭВМ прошлой информации;  – обозначение операции определения знака выражения.
– обозначение операции определения знака выражения.
Преимущества комбинированных робастных систем:
1. Комбинированные системы точнее находят экстремум, по сравнению с безмодельными алгоритмами, за счет наличия блока оптимизации, который отсутствует в безмодельном алгоритме управления;
2. Комбинированные алгоритмы используют модели объекта управления в виде совокупности статических и динамических характеристик, что позволяет идентифицировать не только направление дрейфа критерия управления, но и уменьшить потери информации.
3. Они позволяют оптимизировать величину шага движения к оптимальному значению управляющего воздействия.
4. Наиболее целесообразно применять комбинированный алгоритм в условиях больших флуктуаций входных параметров, а также в условиях большой инерционности объекта управления.
5. Комбинированные алгоритмы позволяют отслеживать дрейф оптимального режима и вырабатывать управляющее воздействие, компенсирующее этот дрейф. В отличие от алгоритма первого типа комбинированные алгоритмы точнее и надежнее.
ПРОБЛЕМЫ:
1. Достоверность показаний виртуальных приборов комбинированных робастных систем зависит не столько от сложности математической модели объекта управления, сколько от точности и чувствительности применяемых технических средств измерения. Под показаниями виртуального прибора понимается решение упрощенной эталонной модели объекта управления.
2. При этом на первый план выдвигаются, упрощение полной эталонной модели до «возможностей системы» и возможностей алгоритмов визуализации процессов измерения и управления.
3. проблемой является количественно обоснованный выбор критериев управления и диагностика эффективности работы энергооборудования.
Пример 11.3. Комбинированная робастная система управления процессом непрерывного розлива стали. Анализ технологического процесса непрерывного розлива стали показал, что для повышения качества продукции необходимо поддерживать постоянным уровень металла, H (t), в кристаллизаторе, который способствует уменьшению количества неметаллических примесей и провалов металла под кристаллизатором. Уровень металла в кристаллизаторе может поддерживаться с помощью двух основных регулируемых параметров – это скорости вытяжки, V(t), заготовки из кристаллизатора и расход металла, G (t), в кристаллизатор. Температурный профиль по высоте кристаллизатора регулируется системой охлаждения, для оптимального функционирования которой необходим прогноз температуры внутренней стенки кристаллизатора. Для этих целей и предлагается математическая модель, адекватность которой подтверждена данными пассивного эксперимента, полученными на реальном объекте управления.
За эталонную модель профиля температур по габаритным размерам кристаллизатора  вязкого жидкого металла, движущегося внутри кристаллизатора со скоростью
вязкого жидкого металла, движущегося внутри кристаллизатора со скоростью 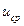 =
=
 ,
,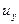 ,
,
 . Где
. Где  ,
,  ,
, 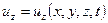 принято уравнение теплопроводности:
принято уравнение теплопроводности:
 , (1)
, (1)
где  - плотность расплава;
- плотность расплава;  - удельная теплоёмкость металла;
- удельная теплоёмкость металла; 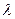 - коэффициент теплопроводности [1]. Пусть геометрические параметры кристаллизатора имеют вид:
- коэффициент теплопроводности [1]. Пусть геометрические параметры кристаллизатора имеют вид:
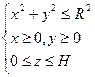 ,
,
Для целей управления целесообразно использовать математическое описание процесса конвективного теплообмена, которое состоит из уравнения неразрывности (2) и трех уравнений движения по пространственным координатам (3 -:- 6). В частности, для потока несжимаемого жидкого металла, при условии, что вязкая диссипация (рассеяние) энергии пренебрежимо мала, эти уравнения имеют вид:
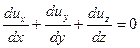 ; (2)
; (2)
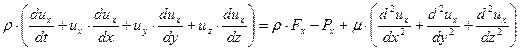 ; (3)
; (3)
 ; (4)
; (4)
 , (5) где
, (5) где  - компоненты массовых сил;
- компоненты массовых сил; 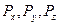 - компоненты поверхностных сил;
- компоненты поверхностных сил;  - плотность;
- плотность; 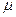 - коэффициент динамической вязкости.
- коэффициент динамической вязкости.
Если составляющие функции скорости определить как:
 , (6)
, (6)
Результаты расчётов переходных процессов по математической модели кристаллизатора (1 -:- 6) с диаметром изложницы 20 см., представлены на слайде 82, где пространственная координата Z – это уровень металла в кристаллизаторе, м.
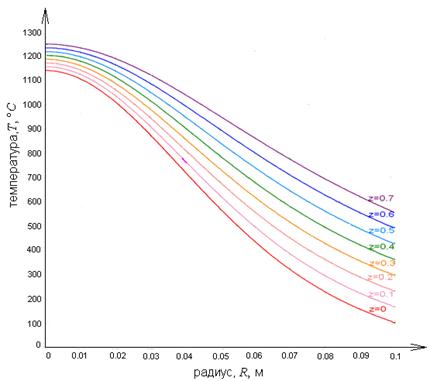
Слайд 82. - Переходные процессы вдоль радиуса кристаллизатора
Прогноз температуры внешней стенки кристаллизатора позволяет определить задачу эффективности функционирования кристаллизатора системой двух алгебраических уравнений параболического вида:
 |
Анализ решения этой системы уравнения показывает, что модель может быть выбрана в качестве критерия управления кристаллизатором, так как имеется минимум по основному управляющему воздействию (расход металла) и максимум по вспомогательному контуру регулирования (скорость протяжки). При этом оба контура должны быть синхронизированы, так как скорость протяжки фактически пропорциональна расходу металла. На слайде 83 видно, что критерий управления представляет собой седло Лагранжа, по которому видно, что оптимальное управление находится в точке с координатами, которые соответствуют минимальному значение расхода сплава и максимальному значению скорости вытяжки.

С лайд 83. Визуализация критерия управления в процессе розлива стали
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 350; Нарушение авторских прав?; Мы поможем в написании вашей работы!