Степенные ряды. Степенным рядом называется ряд вида

Степенным рядом называется ряд вида

где a₀, a₁, a₂,..., a_n - const, x₀ - const.

Рассмотрим вначале более простой случай ряда, когда x₀=0.

(4)

Теорема Абеля. Если ряд (4) сходится при некотором значении x₀, то он сходится абсолютно для всех x, удовлетворяющих условию

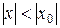(5)

Если ряд (4) расходится при некотором значении x₀, то он расходится для всех x, удовлетворяющих условию

.

Доказательство. Пусть ряд (4) сходится при некотором значении x₀. Это значит, что существует сумма ряда Следовательно, выполняется необходимый признак сходимости

Это значит, что для любого e>0 существует номер N такой, что при всех n> N выполняется неравенство

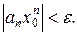
Рассмотрим остаток ряда (4)

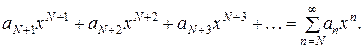
Из неравенства (5) следует, что

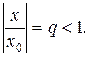
Тогда

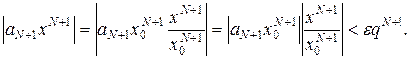
Мы видим, что остаток ряда (4) мажорируется геометрической бесконечно-убывающей прогрессией. Следовательно, ряд (4) сходится. Первая часть теоремы доказана. Вторая часть доказывается аналогично. Разобрать самостоятельно.

Из теоремы Абеля следует, что область сходимости ряда (4) имеет вид -R<x<R, где R>0. При çxç>R ряд (4) расходится. Концы интервала x= -R и x=R могут входить, а могут и не входить в интервал сходимости. Если R=0, то область сходимости состоит из одной единственной точки x=0, Если R=¥, то область сходимости вся числовая ось (-¥;¥).

Дата добавления: 2014-01-14