Кондуктивный теплообмен в плоской стенке

Основное уравнение теплопередачи

Основное уравнение теплопередачи выражает общую зависимость для процессов теплопередачи, выражающее связь между тепловым потоком Q’ и поверхностью теплообмена F:

Q’ = KFDt_срt

K — коэффициент теплопередачи, определяющий среднюю скорость передачи тепла вдоль всей поверхности теплообмена; Dt_ср — средняя разность температур между теплоносителями, определяющая среднюю движущую силу процесса теплопередчи, или температурный напор; t — время.

Физический смысл уравнения: количество тепла, передаваемое от более нагретого к менее нагретому теплоносителю, пропорционально поверхности теплообмена F, среднему температурному напору Dt_ср и времени t.

Для непрерывных процессов теплообмена:

Q = Q’/t = KFDt_ср

Отсюда коэффициент теплопередачи:

K = Q / (FtDt) == ккал / (м²∙ч∙град)

Коэффициент теплопередачи показывает, какое количество тепла (в Дж) переходит за 1 секунду от более нагретого к менее нагретому теплоносителю через поверхность теплообмена 1 м³ при средней разности температур между теплоносителями 1 градус.

Т

Рассмотрим плоскую стенку из однородного

Т₁ материала. Общее уравнение нестационарной

теплопроводности Фурье имеет вид:

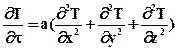λ Т₂ (4.1)

δ

x

рис.4.1

Процесс стационарный, тогда 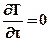, считаем, что высота и длина стенки гораздо больше толщины стенки 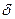, следовательно .

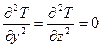Поскольку 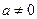, имеем:

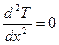(4.2)

Очевидным решением этого уравнения является:

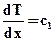
откуда:

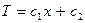(4.3)

Из полученного уравнения 4.3 видно, что в плоской стенке распределение Т является прямолинейным.

Граничные условия:

при ,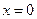

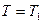при .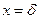

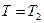Находим 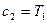и , .

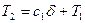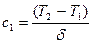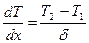(4.4)

Распределение T по толщине :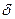

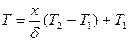(4.5)

Поток тепла за счет теплопроводности определяется по закону Фурье:

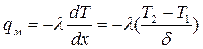(4.6)

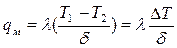(4.7)

Здесь 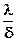- характеризует тепловую проводимость стенки, а 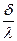- термическое сопротивление стенки.

Для многослойной стенки:

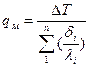(4.8)

Количество теплоты: 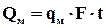(4.9)

Расход тепла:

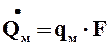(4.10)

Здесь F – поверхность пластины, t – время.

4.1.2. Кондуктивный теплообмен в цилиндрической стенке.

Исходное уравнение в цилиндрической системе координат .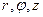

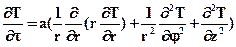(4.11)

T₁

T₂

rr

R₂

Рис.4.3

Считаем, что процесс теплообмена стационарный и длина цилиндра достаточно велика для того, чтобы пренебречь потоком тепла к его торцам вдоль оси 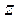. При этих условиях температура является функцией только одной координаты – радиуса :

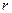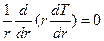или

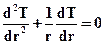(4.12)

Написав уравнение (4.12) в виде:

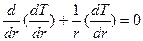
и разделив переменные, получаем:

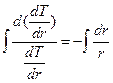
Выполняя интегрирование, находим:

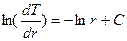
Положив, что С= ln C₁,где С₁ – некоторая новая постоянная, получаем:

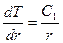
Вторичное интегрирование дает:

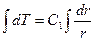
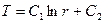(4.13)

Постоянные интегрирования находим из граничных условий:

при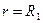

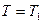
при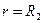

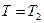
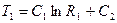
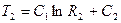
Отсюда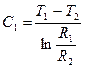

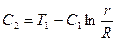
Окончательно: 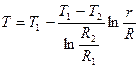(4.14)

Как видно из (4.14) имеет место логарифмический закон распределения температуры по радиусу цилиндра.

Градиент температуры на внутренней поверхности цилиндра равен:

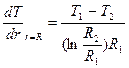
Поток тепла за счет теплопроводности

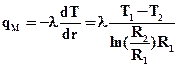(4.15)

Количество теплоты:

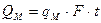(4.16)

Здесь F – внутренняя поверхность цилиндра, t – время.

Расход тепла

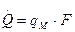(4.17)

Если труба многослойная:

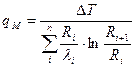(4.18)

Здесь 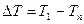- общая разница температуры.

4.1.3 Конвективный теплообмен в плоском пограничном слое и трубах при ламинарном и турбулентном режимах течения.

При конвекции перенос теплоты происходит макрообъемными частицами потока теплоносителя. Конвекция всегда сопровождается теплопроводностью. Как известно, теплопроводность – явление молекулярное, конвекция – явление макроскопическое, при котором в переносе теплоты участвуют целые слои теплоносителя с разными температурами. Конвекцией теплота переносится намного быстрее, чем теплопроводностью. Конвекция у поверхности стенки аппарата затухает.

Конвективный перенос теплоты описывается уравнением Фурье-Кирхгофа.

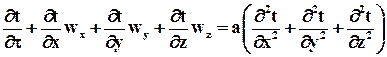
Однако это уравнение приходится решать совместно с уравнением Навье-Стокса (ламинарный режим) и Рейнольдса (турбулентный режим), а также уравнением неразрывности. Возникает так называемая сопряженная задача. В последнее время разработаны аналитические решения основных задач теплоотдачи к ламинарным потокам жидкости с учетом зависимости физических свойств жидкости от температуры. Для турбулентных течений все сложнее, однако, можно использовать приближения, численные решения с помощью компьютерных технологий.

Для упрощения описания процесса переноса тепла, часто рассматривают модель пограничного слоя. По этой модели около стенки существует пограничный слой толщиной (дельта), в котором механизм переноса только молекулярный, т.е. тепло передается теплопроводностью.

Для интенсификации процесса теплообмена необходимо уменьшить величину пограничного слоя.

В общем случае для определения коэффициента теплоотдачи используется обобщенная критериальная зависимость:

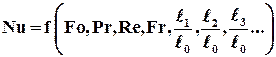
Здесь

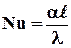– критерий Нуссельта, который характеризует подобие процессов теплопереноса не границе между стенкой и потоком жидкости.

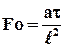– критерий Фурье, необходимое условие подобия неустановившихся процессов теплообмена.

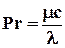– критерий Прандля, характеризует подобие физических свойств теплоносителей в процессах конвективного теплообмена.

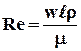– критерий Рейнольдса, характеризует меру отношения сил инерции к силам вязкого трения.

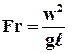– критерий Фруда, отражает влияние сил тяжести на движение жидкости.

В случае установившегося напорного течения жидкости по трубам критериальное уравнение для определения коэффициента теплоотдачи принимает вид:

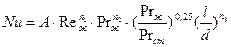(4.31)

Множителем (отношение прандля) учитывается различие поля температур, вязкости и толщины пограничного слоя при нагревании и охлаждении теплоносителя.

Для примера в турбулентном режиме для расчета 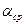при движении потока вдоль плоской стенки предлагается формула:

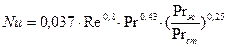(4.34)

При развитом турбулентном течении в трубах и каналах рекомендуется формула:

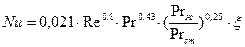(4.35)

Если 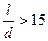, то 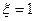, если 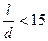, то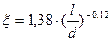

Дата добавления: 2014-01-14