
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Устойчивость сжатых стержней
|
|
|
|
19.1. Основные понятия. Устойчивое и неустойчивое равновесие
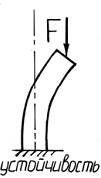 В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых один или два размера поперечного сечения малы по сравнению с длиной стержня. Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней. Опыт показывает, что при достижении сжимающей силой F некоторой критической величины, равной Fкр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении Fкр стержень начинает интенсивно искривляться (выпучиваться). При этом новым (моментным) равновесным состоянием упругого длинного стержня (при F>Fкр) становится некоторая новая уже криволинейная форма. Это явление носит название потери устойчивости.
В конструкциях и сооружениях большое применение находят детали, являющиеся относительно длинными и тонкими стержнями, у которых один или два размера поперечного сечения малы по сравнению с длиной стержня. Поведение таких стержней под действием осевой сжимающей нагрузки оказывается принципиально иным, чем при сжатии коротких стержней. Опыт показывает, что при достижении сжимающей силой F некоторой критической величины, равной Fкр, прямолинейная форма равновесия длинного стержня оказывается неустойчивой, и при превышении Fкр стержень начинает интенсивно искривляться (выпучиваться). При этом новым (моментным) равновесным состоянием упругого длинного стержня (при F>Fкр) становится некоторая новая уже криволинейная форма. Это явление носит название потери устойчивости.
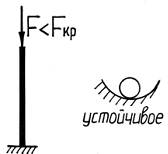
Устойчивость – способность тела сохранять положение или форму равновесия при внешних воздействиях.
Обычно потеря устойчивости системы сопровождается большими перемещениями, возникновением пластических деформаций или разрушением. Возможны также случаи, когда система, потеряв устойчивость, переходит в режим незатухающих колебаний. Особая опасность потери устойчивости заключается в том, что она происходит внезапно и при низких значениях напряжений, когда прочность материала еще далеко не исчерпана.
 При анализе устойчивости конструкций следует различать устойчивое и неустойчивое равновесие системы.
При анализе устойчивости конструкций следует различать устойчивое и неустойчивое равновесие системы.
При устойчивом равновесии тело, выведенное какой-либо силой из своего первоначального положения, возвращается в это положение после прекращения действия силы.
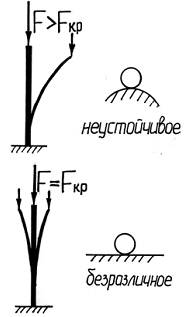
При неустойчивом равновесии тело, выведенное какой-либо силой из своего первоначального положения, продолжает деформироваться в направлении данного ему отклонения, и, после удаления внешнего воздействия, в исходное состояние не возвращается. В этом случае
 говорят, что произошла потеря устойчивости.
говорят, что произошла потеря устойчивости.
Между этими двумя состояниями существует переходное состояние, называемое критич еским, при котором деформированное тело находится в безразличном равновесии: оно может сохранить первоначальную форму, но может и потерять ее от самого незначительного возмущения.
Критическая сила (Fкр) – нагрузка, превышение которой вызывает потерю устойчивости первоначальной формы (положения) тела.
С момента наступления критического состояния до момента разрушения деформации системы нарастают крайне быстро, и практически нет времени принять меры по предотвращению грозящей катастрофы. Таким образом, при расчете на устойчивость критическая нагрузка подобна разрушающей при расчете на прочность.
При этом условие устойчивости можно записать в следующем виде:

19.2. Устойчивость сжатого стержня. Задача Эйлера
При определении критической силы, вызывающей потерю устойчивости сжатого стержня, предполагается, что стержень идеально прямой и сила F приложена строго центрально.
Рассматриваемый метод решения основан на том, что при достижении силой F критического состояния (F=Fкр) стержень находится в безразличном состоянии и ему присущи две формы равновесия: прямолинейная и криволинейная (в таких случаях говорят, что происходит ветвление, или бифуркация, равновесных состояний). Для выявления криволинейной формы равновесия достаточно приложить к стержню малую поперечную возмущающую нагрузку Q, которая вызовет малый прогиб. Если F<Fкр, то
 при удалении Q стержень будет сохранять прямолинейную форму равновесия. Если F>Fкр, то равновесие стержня становится неустойчивым и сколь угодно малое возмущение достаточно для того, чтобы возникли большие прогибы. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил академик Петербургской Академии наук Л. Эйлер в 1744 году.
при удалении Q стержень будет сохранять прямолинейную форму равновесия. Если F>Fкр, то равновесие стержня становится неустойчивым и сколь угодно малое возмущение достаточно для того, чтобы возникли большие прогибы. Задачу о критической нагрузке сжатого стержня с учетом возможности существования двух форм равновесия при одном и том же значении силы решил академик Петербургской Академии наук Л. Эйлер в 1744 году.
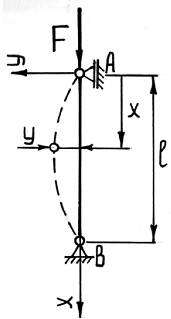
Рассмотрим шарнирно опертый по концам стержень, сжатый продольной силой F. Положим, что по какой-то причине стержень получил малое искривление оси, вследствие чего в нем появился изгибающий момент M:
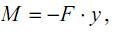
где y – прогиб стержня в произвольном сечении с координатой x.
Для определения критической силы можно воспользоваться приближенным дифференциальным уравнением упругой линии:

где E – модуль Юнга; J – осевой момент инерции сечения стержня относительно оси z в данном случае; E·J – жесткость стержня при изгибе. Знаки левой и правой части (19.2) согласованны в данной системе координат.
Подставив в это уравнение выражение для изгибающего момента (19.1), получим

Общий интеграл полученного однородного дифференциального уравнения представляется функцией
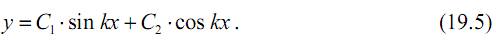
Это решение содержит три неизвестные: постоянные интегрирования С1 и С2 и параметр k. Найдем эти величины из граничных условий – условий закрепления стержня по концам:
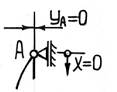 а) при x=0 прогиб в опоре (точка A) должен быть равен нулю y=0, тогда из уравнения (19.5) получим, что С2=0, при этом формула приобретает вид
а) при x=0 прогиб в опоре (точка A) должен быть равен нулю y=0, тогда из уравнения (19.5) получим, что С2=0, при этом формула приобретает вид

Уравнение (19.6) указывает на то, что при продольном изгибе изогнутая ось стержня может быть представлена как некоторое число волн синусоиды с амплитудой C1.
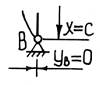 б) при x=l прогиб в другой опоре (точка B) должен быть также равен нулю y=0, тогда из уравнения (19.6) получим, что
б) при x=l прогиб в другой опоре (точка B) должен быть также равен нулю y=0, тогда из уравнения (19.6) получим, что 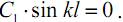 Согласно постановке задачи, коэффициент C1 заведомо не равен нулю (иначе равен нулю прогиб балки во всех точках, что противоречит постановке задачи). В этом случае получаем
Согласно постановке задачи, коэффициент C1 заведомо не равен нулю (иначе равен нулю прогиб балки во всех точках, что противоречит постановке задачи). В этом случае получаем
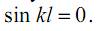
Из свойств синусоиды следует, что

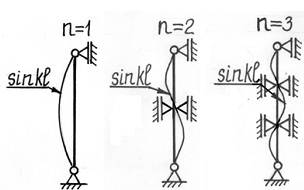 где n – произвольное целое число (n≠0), которое представляет собой число полуволн синусоиды, укладывающихся на длине изогнутой оси стержня.
где n – произвольное целое число (n≠0), которое представляет собой число полуволн синусоиды, укладывающихся на длине изогнутой оси стержня.
Решая совместно уравнения (19.4) и (19.7), получим выражение для некоторых фиксированных значений сжимающей силы, при которых возможна криволинейная форма равновесия оси стержня
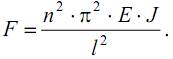
Как видим, минимальное значение критическая сила примет при n=1 (на длине стержня укладывается одна полуволна синусоиды) и J=Jmin (стержень искривляется относительно оси с наименьшим моментом инерции)

Это выражение обычно называют форм улой Эйлера, а определяемую с ее помощью критическую силу – эйлеровой силой.
19.3. Зависимость критической силы от условий закрепления стержня
 Формула Эйлера была получена нами для, так называемого, основного случая – в предположении шарнирного опирания стержня по концам. На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, согласно (19.8), при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды.
Формула Эйлера была получена нами для, так называемого, основного случая – в предположении шарнирного опирания стержня по концам. На практике встречаются и другие случаи закрепления стержня. При этом можно получить формулу для определения критической силы для каждого из этих случаев, решая, как в предыдущем параграфе, дифференциальное уравнение изогнутой оси балки с соответствующими граничными условиями. Но можно использовать и более простой прием, если вспомнить, что, согласно (19.8), при потере устойчивости на длине стержня должна укладываться одна полуволна синусоиды.
Рассмотрим некоторые характерные случаи закрепления стержня по концам и получим общую формулу для различных видов закрепления.
 1-й случай
1-й случай
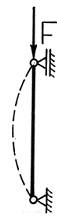
Стержень длиной l заделан одним концом и сжат продольной силой. Из сравнения вида изогнутой оси балки для рассматриваемого и основного случаев можем сделать вывод, что ось стержня, заделанного одним концом, находится в тех же условиях, как и верхняя половина шарнирно опертого стержня длиной 2·l. Таким образом, критическая сила для стержня длиной l с одним защемленным концом может быть найдена так же как и для шарнирно опертой балки длиной 2·l, то есть
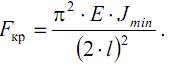
 2-й случай
2-й случай
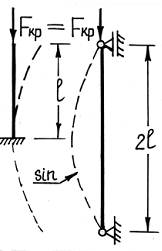
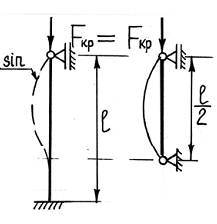
Стержень длиной l, у которого оба конца жестко заделаны. Из сравнения вида изогнутой оси балки для рассматриваемого и основного случаев, а также из соображений симметрии, можем сделать вывод, что средняя часть стержня с заделанными концами, находится в тех же условиях, как и шарнирно опертая балка длиной l/2.
Таким образом, критическая сила для стержня длиной l с двумя защемленными концами может быть найдена так же как и для шарнирно опертой балки длиной l/2, то есть
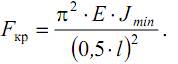
 3-й случай
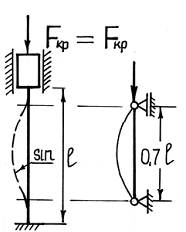
3-й случай
Стержень длиной l, у которого один конец жестко заделан, а другой шарнирно оперт. Из сравнения вида изогнутой оси балки для рассматриваемого и основного случаев, можем сделать вывод, что часть стержня находится в тех же условиях, как и шарнирно опертая балка длиной 0,7·l. Таким образом, критическая сила для стержня длиной l с защемленным и шарнирно опертым концами может быть найдена так же как и для шарнирно опертой балки длиной 0,7·l, то есть
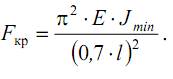
Все полученные выражения можно объединить в одну общую формулу

где ω·l=lпр – приведенная длина стержня; l – фактическая длина стержня; ω – коэффициент приведенной длины, показывающий во сколько раз необходимо изменить длину стержня, чтобы критическая сила для этого стержня стала равна критической силе для шарнирно опертой балки.
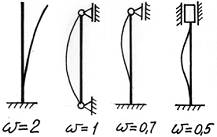 (Другая интерпретация коэффициента приведенной длины: ω показывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)
(Другая интерпретация коэффициента приведенной длины: ω показывает, на какой части длины стержня для данного вида закрепления укладывается одна полуволна синусоиды при потере устойчивости.)
19.4. Критические напряжения. Расчет на устойчивость стержня при упруго-пластических деформациях
Введем понятие критического напряжения, то есть напряжения, соответствующего критической силе при потере устойчивости сжатого стержня
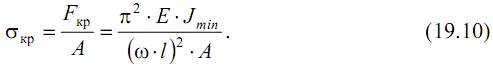
Вспомним, что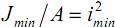 – квадрат минимального радиуса инерции. Тогда формулу (19.10) можно записать так:
– квадрат минимального радиуса инерции. Тогда формулу (19.10) можно записать так:
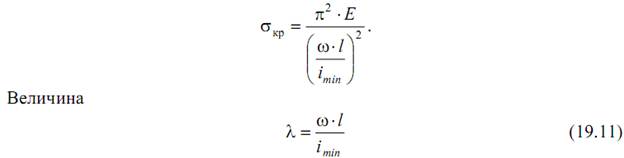
называется гибкостью стержня.
Окончательно получим

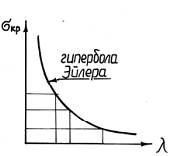 Как видим, критическое напряжение зависит только от упругих свойств материала (модуля Юнга E) и гибкости стержня λ. При этом зависимость между σкр и λ может быть представлена гиперболической кривой, называемой гиперболой Эйлера.
Как видим, критическое напряжение зависит только от упругих свойств материала (модуля Юнга E) и гибкости стержня λ. При этом зависимость между σкр и λ может быть представлена гиперболической кривой, называемой гиперболой Эйлера.
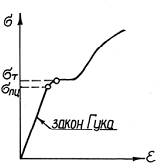 Вывод формулы Эйлера основан на применении дифференциального уравнения упругой линии балки. Поэтому использовать эту формулу можно лишь в том случае, когда деформирование материала протекает в соответствии с законом Гука, то есть пока критическое напряжение не превысит предела пропорциональности σпц (по диаграмме сжатия материала):
Вывод формулы Эйлера основан на применении дифференциального уравнения упругой линии балки. Поэтому использовать эту формулу можно лишь в том случае, когда деформирование материала протекает в соответствии с законом Гука, то есть пока критическое напряжение не превысит предела пропорциональности σпц (по диаграмме сжатия материала):

Используя это соотношение, можно найти условие для определения предельной гибкости стержня λпр, когда еще возможно применение формулы Эйлера:

Например, для малоуглеродистых сталей (E=2·105 МПа, σпц≈200 МПа) предельная гибкость
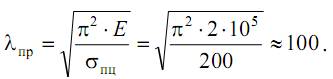
Итак, при λ>λпр для определения критической силы будем пользоваться формулой Эйлера, если же λ<λпр, то формула Эйлера становится неприемлемой, так как дает завышенные значения критической силы, то есть всегда переоценивает действительную устойчивость стержней.
Поэтому использование формулы Эйлера для стержней, теряющих устойчивость за пределом пропорциональности не только неправильно, но и опасно.
Теоретическое решение задачи об устойчивости за пределом пропорциональности сложно, поэтому для расчетов на устойчивость в этой области обычно пользуются эмпирическими формулами, полученными в результате обработки большого числа экспериментальных данных.
Прежде всего, выделим стержни с малой гибкостью, у которых  (для стали). Эти короткие стержни будут выходить из строя главным образом за счет потери прочности, потеря устойчивости в таких случаях, как правило, не наблюдается. Таким образом, для стержней малой гибкости при сжатии проводят обычный расчет на прочность, принимая в качестве предельного напряжения предел текучести (для пластичных материалов) или предел прочности σв (для хрупких материалов). Этому условию соответствует горизонтальная прямая на рисунке.
(для стали). Эти короткие стержни будут выходить из строя главным образом за счет потери прочности, потеря устойчивости в таких случаях, как правило, не наблюдается. Таким образом, для стержней малой гибкости при сжатии проводят обычный расчет на прочность, принимая в качестве предельного напряжения предел текучести (для пластичных материалов) или предел прочности σв (для хрупких материалов). Этому условию соответствует горизонтальная прямая на рисунке.
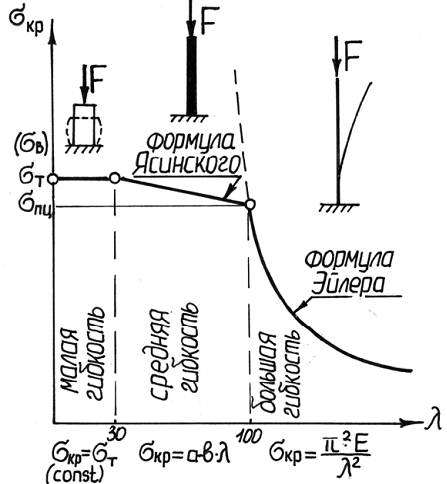
Для практических (инженерных) расчетов стержней средней гибкости 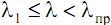 чаще всего используется эмпирическая зависимость, предложенная Ф. С. Ясинским на основе изучения опытных данных (формула Ясинского):
чаще всего используется эмпирическая зависимость, предложенная Ф. С. Ясинским на основе изучения опытных данных (формула Ясинского):

где a и b – эмпирические коэффициенты, зависящие от материала (например, для стали 40: a=321 МПа, b=1,16 МПа). Формуле Ясинского на диаграмме критических напряжений соответствует наклонная прямая.
19.5. Определение допускаемых напряжений на устойчивость. Коэффициент понижения напряжений
Как видим, для продольно сжатых стержней необходимо проводить две проверки:
а) проверка на прочность
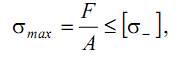
где 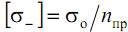 – допускаемое напряжение на сжатие; σо – опасное напряжение (предел текучести для пластичных материалов или предел прочности для хрупких); nпр – коэффициент запаса прочности.
– допускаемое напряжение на сжатие; σо – опасное напряжение (предел текучести для пластичных материалов или предел прочности для хрупких); nпр – коэффициент запаса прочности.
б) проверка на устойчивость

где 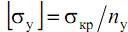 – допускаемое напряжение на устойчивость; σкр – критическое напряжение на устойчивость; nу – коэффициент запаса устойчивости.
– допускаемое напряжение на устойчивость; σкр – критическое напряжение на устойчивость; nу – коэффициент запаса устойчивости.
Отметим, что коэффициент запаса устойчивости (для сталей nу=1,8...3) всегда выше коэффициента запаса на прочность (nпр=1,4...1,6). Это объясняется тем, что коэффициент запаса устойчивости, кроме всего прочего, зависит от таких факторов, как начальная кривизна стержня, эксцентриситет приложения нагрузки, неоднородность материала, которые незначительно влияют на прочность, однако могут вызвать преждевременную потерю устойчивости.
Сравнивая выражения для допускаемых напряжений на устойчивость и прочность, установим связь между этими напряжениями

Введем следующее обозначение

где ϕ – коэффициент понижения основного допускаемого напряжения при расчете на устойчивость.

Коэффициент ϕ зависит от марки материала и гибкости λ стержня и приводится в справочных таблицах.
Таким образом, окончательно условие устойчивости примет вид

Рассмотрим два вида расчета на устойчивость сжатых стержней – проверочный и проектировочный.
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 9904; Нарушение авторских прав?; Мы поможем в написании вашей работы!