Пример расчета плоской рамы методом перемещений на силовое воздействие в матричной форме

Для концевых сечений элементов статически неопределимой рамы (рис. 22.5) вычислить расчетные изгибающие моменты и соответствующие им поперечные и продольные силы. Постоянная нагрузка показана на рис. 22.5,а, временная – на рис. 22.5,б. Соотношение между изгибными жесткостями поперечных сечений стержней рамы известно:

EJ_ab: EJ_eС: EJ_aе: EJ_Aa = 2: 2: 1: 1,25.

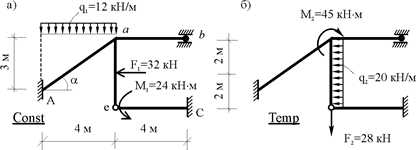
Рис. 22.5

Порядок расчета рамы в матричной форме на заданное силовое воздействие определяется соотношением (22.27):

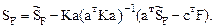
1. Подготовительный этап расчета: определение степени кинематической неопределимости рамы (n_kin = n_θ + n_Δ = 1+1 = 2), выбор основной системы метода перемещений (рис. 22.6,а), построение в основной системе метода перемещений деформационных схем элементов рамы от единичных смещений наложенных связей (рис. 22.6,б,в) и эпюр изгибающих моментов от постоянной и временной нагрузок (рис. 22.6,г,д). Читателям предлагается все операции подготовительного этапа выполнить самостоятельно, повторив, при необходимости, основные положения девятнадцатой лекции.

2. Нумерация стержней рамы и их концевых сечений (рис. 22.7). В скобках около номеров концевых сечений указаны концевые усилия (изгибающие моменты и поперечные силы), которые в дальнейшем будут вычисляться при формировании матрицы 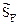. Указанный порядок вычисления концевых усилий позволяет использовать для расчета рамы стандартные матрицы внутренней жесткости ее элементов, полученные в п. 22.3 настоящей лекции.

3. Вычисление погонных жесткостей стержней рамы. Сохраняя соотношение между изгибными жесткостями поперечных сечений элементов рамы, будем считать:

EJ_ab = EJ_eС = 8, EJ_ae = 4, EJ_Aa = 5.

Относительные погонные жесткости стержней рамы в этом случае примут следующие значения:

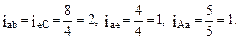
4. Формирование матриц K и a и вычисление матрицы коэффициентов при неизвестных 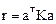системы канонических уравнений метода перемещений. Используем стандартные матрицы внутренней жесткости элементов рамы, полученные в п. 22.3.

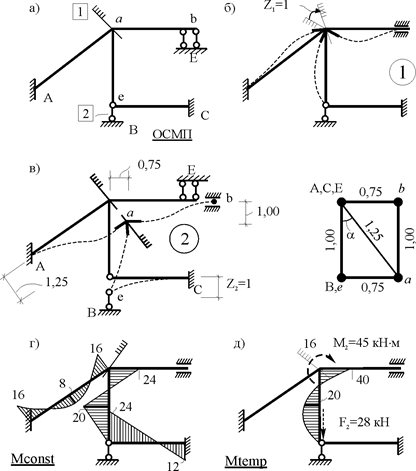
Рис. 22.6

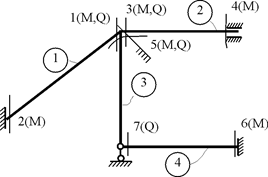
Рис. 22.7

Для первого (наклонного) стержня (рис. 22.7) при i = 1

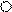
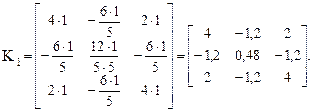
Для второго (верхнего горизонтального) стержня при i = 2

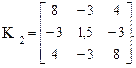
Для третьего (вертикального) стержня при i = 1

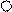
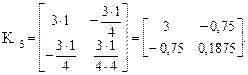
Для четвертого (нижнего горизонтального) стержня при i = 2

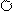
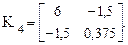
Матрица внутренней жесткости рамы в целом запишется:

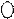
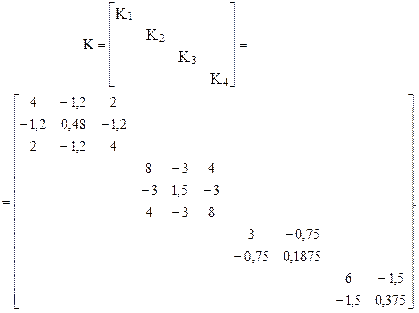
Для формирования матрицы а, – матрицы концевых перемещений стержней от единичных смещений наложенных связей в основной системе метода перемещений, используем деформа­ционные схемы, показанные на рис. 22.6,б,в.

В соответствии с принятой нумерацией стержней рамы и их концевых сечений (рис. 22.7) в первом столбце матрицы а фиксируем повороты концевых сечений и перекосы стержней от единичного смещения угловой связи по часовой стрелке (рис. 22.6,б), а во втором – эти же перемещения, но от единичного смещения линейной связи, наложенной на узел e, вниз (рис. 22.6,в). При этом полезно помнить, что в основной системе метода перемещений от смещения угловых связей отсутствуют перекосы стержней, а от смещения линейных связей – повороты концевых сечений стержней.

Напомним читателям правило знаков для концевых перемещений (см. п. 22.1 настоящей лекции): повороты концевых сечений считаются положительными, если они происходят по часовой стрелке, и отрицательными, – если против часовой стрелки; перекос стержня считается положительным, если его поворот совершается по часовой стрелке, и отрицательным, – если против.

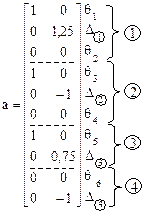
Транспонированная матрица имеет вид:

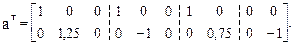
Имея матрицы а^т, K, а, вычислим матрицу внешней жесткости сооружения, или матрицу коэффициентов при неизвестных системы канонических уравнений метода перемещений.

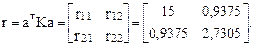
5. Обращение матрицы внешней жесткости сооружения (см. п. 16.8 третьей части лекций по строительной механике стержневых систем).

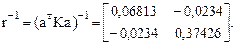
6. Формирование матриц 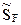, F, с и вычисление матрицы свободных членов системы канонических уравнений метода перемещений R_F.

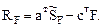
Элементы матрицы концевых усилий стержней рамы 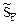получим, используя эпюры изгибающих моментов M_const (рис. 22.6,г) и M_temp (рис. 22.6,д), полученные в основной системе метода перемещений от заданных нагрузок. Концевые изгибающие моменты и поперечные силы фиксируем в порядке, установленном нумерацией концевых сечений стержней рамы и последовательностью их записи. Правило знаков для концевых усилий было установлено в п. 22.1 настоящей лекции: концевой изгибающий момент и концевая поперечная сила считаются положительными, если они вращают стержень по часовой стрелке, и отрицательными, – если против часовой стрелки. Для вычисления концевых поперечных сил используются уравнения равновесия для отдельных стержней (см. п. 5.4 первой части лекций по строительной механике стержневых систем). В первом столбце матрицы 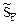записываются концевые усилия от постоянной нагрузки, во втором – от временной нагрузки.

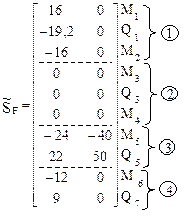
Формированию матрицы узловых нагрузок F предшествует перенос равнодействующих нагрузок, приложенных к отдельным стержням, на узлы, расположенные противоположно концевым сечениям, в которых при формировании матрицы 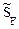фиксировались концевые поперечные силы (рис. 22.8). Обход узлов производится в строго установленном порядке, например, узлы А, а, b, e, C (рис. 22.8). С целью сокращения числа строк в матрице F можно не принимать во внимание узлы, к которым во всех сочетаниях нагрузок не приложены сосредоточенные силы и сосредоточенные моменты, т.е. можно не фиксировать нулевые значения этих узловых воздействий. В нашем примере – это узлы b и С (рис. 22.8). В дополнение к этому в матрицу F не следует включать сосредоточенные силы, действующие на узлы, не имеющие в заданном сооружении линейных перемещений, так как работа этих сил на перемещениях таких узлов равна нулю (см. формулировку теоремы о работе концевых усилий в п. 22.1 настоящей лекции). В рассматриваемом примере – это узел А (рис. 22.8), на который действует вертикальная сосредоточенная сила q₁ּ4 = 48 кН. Таким образом, при формировании матрицы F в нашем случае можно ограничиться описанием узловых нагрузок, действующих на узлы a и e (рис. 22.8).

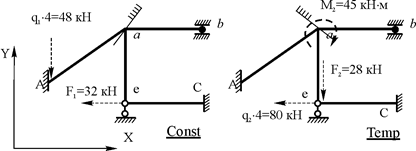
Рис. 22.8

Знаки сосредоточенных узловых сил, включаемых в матрицу F, привязываются к принятой системе координат (оси x и y на рис. 22.8). Сосредоточенные узловые моменты считаются положительными, если они вращают узлы по часовой стрелке, и отрицательными, – если против часовой стрелки.

Условимся для каждого узла сначала записывать горизонтальную сосредоточенную силу, затем – вертикальную сосредоточенную силу, и в последнюю очередь – узловой сосредоточенный момент. При отсутствии во всех сочетаниях внешних силовых воздействий какой-либо из перечисленных компонент ее нулевые значения в матрицу F для рассматриваемого узла можно не включать. Первый столбец матрицы F описывает постоянную узловую нагрузку, второй – временную узловую нагрузку.

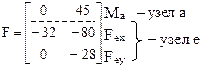
Элементы матрицы c должны описывать перемещения узлов в основной системе метода перемещений в направлении узловых сосредоточенных сил и сосредоточенных моментов, включенных в матрицу F, от единичных смещений наложенных связей. Для формирования матрицы c используем деформационные схемы рамы в основной системе метода перемещений, полученные от смещения наложенных связей на величину, равную единице (рис. 22.6,б,в). Первый столбец этой матрицы включает в себя угол поворота узла а, горизонтальное и вертикальное перемещение узла e от единичного поворота угловой связи (рис. 22.6,б), второй – эти же перемещения от единичного смещения линейной связи (рис. 22.6,в). Поворот узла по часовой стрелке в соответствии с принятым знаком для узловых сосредоточенных моментов считается положительным, знаки же линейных перемещений узлов привязываются к ранее принятой системе координат (рис. 22.8).

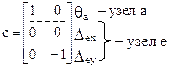
Транспонированная матрица запишется:

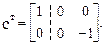
После формирования матриц а^т, 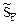, с^т и F получим матрицу свободных членов системы канонических уравнений метода перемещений R_F.

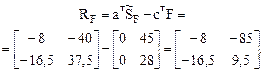
7. Вычисление элементов матрицы неизвестных метода перемещений по формуле (22.22).

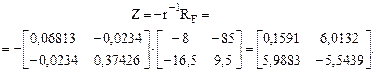
8. Вычисление матрицы концевых усилий в заданной раме по формуле (22.27).

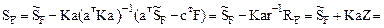
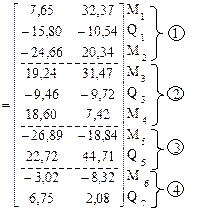
9. Проверка решения по формуле (22.31).

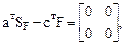
т.е. реакции в наложенных связях в основной системе метода перемещений равны нулю, что соответствует заданному состоянию рамы, где эти связи отсутствуют.

10. Построение эпюр внутренних усилий в заданной раме от постоянной нагрузки (рис. 22.9) и временной нагрузки (рис. 22.10).

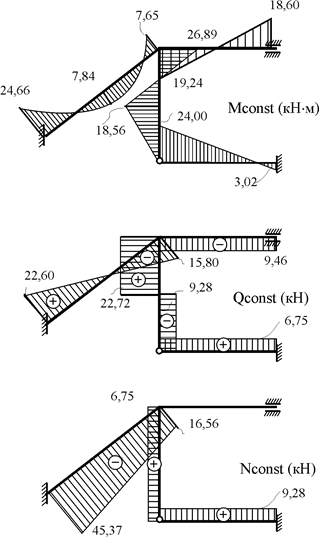
Рис. 22.9

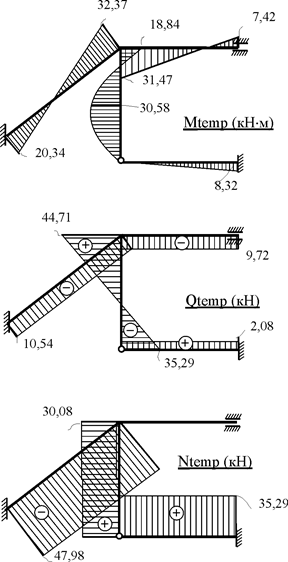
Рис. 22.10

Матрица S_F содержит ординаты эпюр изгибающих моментов для всех концевых сечений стержней рамы и ординаты эпюр поперечных сил для сечений 1, 3, 5, 7. Недостающие ординаты эпюр поперечных сил для первого и третьего элементов рамы от постоянной нагрузки и для третьего элемента от временной нагрузки (рис. 22.7) определяются из условий равновесия перечисленных элементов. Ординаты эпюр продольных сил вычисляются из условий равновесия узлов рамы. Вычисление недостающих ординат эпюры Q и построение эпюры N предлагается выполнить самостоятельно.

11. Вычисление расчетных изгибающих моментов и соответствующих им поперечных и продольных сил (см. таблицу ниже).

	Номера концевых сечений
Mconst	–7,65	–24,66	19,24	–18,60	26,89	3,02
Mtemp	–32,37	20,34	31,47	–7,42	18,84	8,32
Qconst	–15,80	22,60	–9,46	–9,46	22,72	6,75
Qtemp	–10,54	–10,54	–9,72	–9,72	44,71	2,08
Nconst	–16,56	–45,37			6,75	9,28
Ntemp	–47,98	–47,98			30,08	35,29
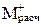
	–	–	50,71	–	45,73	11,34
Qсоотв	–	–	–19,18	–	67,43	8,83
Nсоотв	–	–		–	36,83	44,57
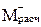
	–40,02	–24,56	–	–26,02	–	–
Qсоотв	–26,34	22,60	–	–19,18	–	–
Nсоотв	–64,54	–45,37	–		–	–

Примечание. 1. Изгибающие моменты, приведенные в таблице, имеют размерность кН∙м, поперечные и продольные силы – кН.

2. На горизонтальных и наклонном элементах рамы положительными зафиксированы изгибающие моменты, растягивающие нижние волокна, а на вертикальном – изгибающие моменты, растягивающие правые волокна.

3. «Прочерк» в таблице означает, что расчетные изгибающие моменты с указанным знаком («плюс» или «минус») при любых сочетаниях постоянной и временной нагрузки будут отсутствовать. В этом случае теряет смысл вычисление соответствующих поперечных и продольных сил.

Дата добавления: 2014-01-14