Основные понятия. Определение. Говорят, что в некоторой области D трехмерного пространства задано скалярное поле, если каждой точке MÎD поставлено в соответствие число

Элементы теории поля

Лекция 25

Определение. Говорят, что в некоторой области D трехмерного пространства задано скалярное поле, если каждой точке MÎD поставлено в соответствие число.

Зададим прямоугольную декартову систему координат Oxyz. Тогда скалярное поле задает некоторую функцию U=U(x,y,z). Для наглядного геометрического изображения скалярного поля используют поверхности уровня. Поверхность уровня - это множество точек области D, для которой функция принимает постоянное значение U(x,y,z)=C, где C=const.

Примеры. Поле распределения температур в неравномерно разогретом теле, поле распределения масс внутри тела.

Определение. Говорят, что в некоторой области D трехмерного пространства задано векторное поле, если каждой точке MÎD поставлен в соответствие вектор F.

Зададим прямоугольную декартову систему координат Oxyz. Обозначим единичные векторы осей Ox,Oy и Oz буквами i, j, k. Тогда в области D векторное поле F задает тройку функций:

F =P(x,y,z) i+Q (x,y,z) j+R (x,y,z) k = (P(x,y,z);Q(x,y,z);R(x,y,z)).

Примеры. Поле распределения скоростей частиц жидкости в области D. Поле распределения напряженностей электростатического поля.

Пусть задано некоторое скалярное поле U=U(x,y,z) и пусть функция U непрерывна и непрерывно дифференцируема.

Определение. Градиентом функции U называется вектор, равный

Вектор градиент в каждой точке перпендикулярен поверхности уровня поля U и показывает направление быстрейшего возрастания функции U. Пусть l - единичный вектор.

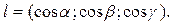
Производная по направлению равна

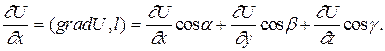
Пусть задано некоторое векторное поле F = (P(x,y,z);Q(x,y,z);R(x,y,z)) и пусть функция P,Q,R непрерывное и непрерывно дифференцируемое.

Определение. Дивиргенцией векторного поля F называется величина, равная

Для случая поля течения жидкостей дивиргенция F показывает мощность источников жидкости в данной точке поля.

Определение. Вихрем или ротором векторного поля F называется вектор, равный

Ротор F показывает величину завихренностиполя.

Определение. Векторное поле F называется потенциальнымв области D, если существует функция U=U(x,y,z) такая, что F = gradU. Функция U называется потенциальной функцией поля.

Пример. Поле распределения напряженностей электростатического поля. Потенциальная функция равна

где j - потенциал электростатического поля.

Напряженность поля равна

Определение. Векторное поле F называется соленоидальнымв области D, если существует векторное поле A такое, что F = rot A. Векторное поле A называется векторным потенциалом поля.

Пример. Поле распределения напряженностей магнитостатического поля.

Введем обозначение

r =(x,y,z)=x i + y j + z k.

Тогда

d r =(dx,dy,dz)= i dx + j dy + k dz.

Определение. Пусть задано некоторое векторное поле F в области D. Зададим некоторый контур L, лежащий в области D. Если F - силовое поле. то интеграл по контуру

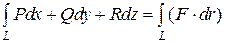
определяет работу силового поля при перемещении тела по контуру L. Если контур L замкнут, то интеграл называется циркуляцией.

Определение. Пусть задано некоторое векторное поле F в области D. Зададим некоторую двустороннюю поверхность, лежащую в области D. Потоком векторного поля через поверхность называется величина

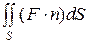
Для случая поля течения жидкостей поток векторного поля F равен количеству жидкости, протекающей через данную поверхность.

Дата добавления: 2014-01-14