Формула Байеса

Постановка задачи та же, но решаем обратную задачу.

Проводится испытание, в результате которого произошло событие A. Какова вероятность того, что в этом испытании произошло событие B_i.

Условные вероятности называются апостериорными, а безусловные - априорными вероятностями.

P(AB_i)=P(A)P(B_i/A)=P(B_i)P(A/B_i)

Откуда,

Таким образом, формула Байеса:

Композиция испытаний.

Имеется вероятностное пространство, которое порождает испытание 1.

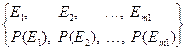
где E_i, i=1,..., m₁ - пространство элементарных событий в результате испытания.

P(E_i), i=1,..., m₁ - вероятности элементарных событий.

Испытание 2 порождает вероятностное пространство вида

P(E_i), P(Q_j) - разные вероятностные меры.

Композицией двух испытаний называется сложное испытание, состоящее в поведении первого и второго испытания.

Композиция испытаний порождает вероятностное пространство вида:

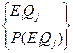
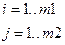
E_iQ_j - композиционное событие.

В общем случае по P(E_i) и P(Q_j) найти P(E_iQ_j) невозможно.

Рассмотрим один частный случай, когда это можно сделать.

Два испытания называются независимыми, если различные исходы обоих испытаний определяются несвязанными между собой случайными факторами.

Из определения независимости испытания вытекает, что условные частости наступления события в одном испытании, при условии, что во втором испытании произошло фиксированное число событий равны безусловным частостям, если они существуют.

Пусть испытания независимы. В результате проведения первого испытания произошло элементарное событие E_i, в результате второго испытания может произойти все что угодно.

Тогда сложное событие, определяющее исход первого и второго испытания имеет вид:

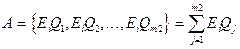и равно сумме комбинаций исходов первого и второго испытаний.

Вероятность сложного события A.

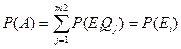, т.е. результаты второго испытания не зависят от результатов первого.

Если в результате второго испытания произошло событие Q_j, а в результате первого испытания могло произойти все что угодно, то сложное событие B имеет вид: .

Вероятность сложного события B равна сумме вероятностей комбинаций вида E_iQ_j, i=1,..., m1

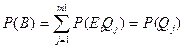, т.к. исходы первого испытания не влияют на исходы второго испытания. Из факта: P(AB)=P(A)P(B/A); P(B/A)=P(B); AB=E_iQ_j (надо доказать)

A={E_iQ₁, E_iQ₂,..., E_iQ_j,..., E_iQ_m2}

B={E₁Q_j, E₂Q_j,..., E_iQ_j,..., E_m1Q_j}

По определению произведения AB в него входят только те события, которые входят и в A, и в B. Из приведенных выше формул следует, что только событие E_iQ_j входит и в A, и в B, то AB= E_iQ_j. Следует:

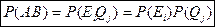
Композиционное пространство имеет вид:

Общая структура независимых событий в композиционном пространстве, порожденном композицией испытаний:

т.е. в результате первого испытания произошли элементарные события: .

В результате второго испытания события: .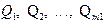

Сложное событие B определяет все возможные комбинации исходов двух испытаний независимо друг от друга. В результате первого испытания произошли элементарные события: .

В результате второго испытания события: .

Тогда: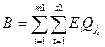

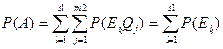, т.к. второе испытание не влияет на результаты первого.

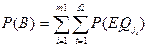
т.к. , (надо доказать)

то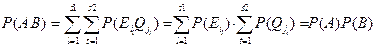

При решении практических задач, связанных с независимыми испытаниями обычно не требуется строить композиционных пространств элементарных событий, а использовать формально неверную запись: P(A×B)=P(A)×P(B).

Композиция n испытаний.

Имеется n испытаний. Зададим для i-го испытания вероятностное пространство:

i=1,..., n

Композицией n испытаний называется сложное испытание, состоящее в совместном проведении n испытаний. Задается n испытаний, вероятностное пространство каждого из которых имеет вид:

i=1,..., n

Композиционное пространство имеет вид:

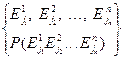j₁=1,..., m₁; j₂=1,..., m₂; j_n=1,..., m_n;

Композиция n независимых испытаний.

Испытания (n - испытаний) называются независимыми, если неоднозначность исхода каждого из испытаний определена не связанными между собой группами факторов.

Событие A₁: в результате проведения композиционного испытания в первом испытании произошло событие 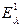. Тогда

Событие A_n: в результате проведения композиционного испытания в первом испытании произошло событие . Тогда

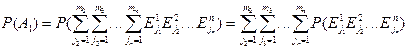
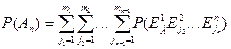
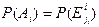i=1,..., n

Рассмотрим событие:

В силу определения независимости испытаний очевидно, что:

.

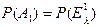
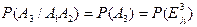
Следовательно: .

На практике не строят композиционных пространств, а записывают формально неправильную формулу: P(A₁A₂...A_n)=P(A₁)P(A₂)...P(A_n).

Композиционное пространство имеет вид:

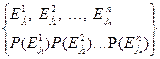j₁=1,..., m₁; j₂=1,..., m₂; j_n=1,..., m_n;

Общая структура независимых событий в композиционном пространстве имеет вид:

1-е событие -	это событие, которое происходит в 1-м вероятностном пространстве
2-е событие -	это событие, которое происходит во 2-м вероятностном пространстве
n - событие -	это событие, которое происходит в n-м вероятностном пространстве

Рассмотрим два вероятностных пространства.

I	II

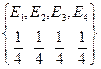
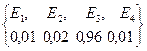
Очевидно, что неопределенность испытания до испытания в первом вероятностном пространстве выше, чем во втором. Действительно, до испытания в I нельзя ни одному из событий отдать предпочтения, а во II событие E₃ происходит чаще.

Энтропия - мера неопределенности исхода испытания (до испытания).

Первым, кто функционально задал выражение для энтропии был Шеннон.

,

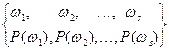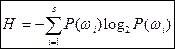
Для вероятностного пространства:

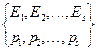
Энтропия задается выражением: 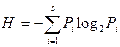. Если P₁=0, то P_i×logPi­=0.

Самим показать, что:

Если вероятностное пространство не имеет определенности, т.е. какое-то из P_i=1, а остальные равны 0, то энтропия равна нулю.

Если элементарный исход равновероятен, т.е. , то энтропия принимает максимальное значение.

0£P_i£1,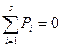

1)

,

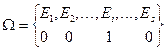
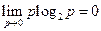
т.о. вероятности p₁, p₂,..., p_s обращаются в ноль, например p_i, которая равна 1. Но log1=0. Остальные числа также обращаются в 0, т.к. .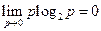

2) Докажем, что энтропия системы с конечным числом состояний достигае максимума, когда все состояния равновероятны. Для этого рассмотрим энтропию системы как функцию вероятностей p₁, p₂,..., p_s и найдем условный экстремум этой функции, при условии, что .

Пользуясь методом неопределенных множителей Лагранжа, будем искать экстремум функции: .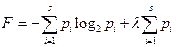

Дифференцируя по p₁, p₂,..., p_s и приравнивая производные нулю получим систему:

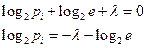i=1,..., s

Откуда видно, что экстремум достигается при равных между собой p₁.

Т.к. , то p₁= p₂=,..., = p_s= 1/s.

Еденицей измерения энтропии является энтропия вероятностного пространства вида: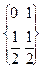

, которая называется 1 бит.

Неопределенность исхода испытания до испытания автоматически определяет информативность исхода испытания после испытания. Поэтому в битах также измеряется информативность исхода.

Рассмотрим два вероятностных пространства:

Проводим композицию двух испытаний. Композиционное пространство имеет вид:

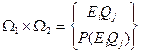i=1,..., s₁ j=1,..., s₂

С точки зрения качественного анализа максимальная энтропия композиционного вероятностного пространства достигается тогда, когда испытания независимы. Найдем энтропию композиционного пространства для случая независимых испытаний.

Биномиальное распределение.

n испытаний называются системой испытаний Бернулли, если испытания независимы, в каждом из них происходит событие 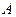, либо 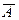с вероятностью наступления P(A) = p;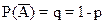

Найдем вероятность того, что в результате проведенных n испытаний событие А произошло m раз:

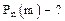
Рассмотрим композицию n независимых испытаний и построим композиционное пространство элементарных событий.

Общий вид элемента этого пространства следующий:

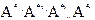
где

При этом вероятность наступления такого события равна:

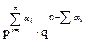(умножение при независимых событиях)

Найдем вероятность наступления любого элементарного события из композиционного пространства:

Рассмотрим в композиционном вероятностном пространстве событие: в n испытаниях событие A произошло m раз.

Событие A состоит из - общее кол-во элементарных событий, в которое входит событие А. А произошло m раз, 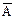- n-m раз. Вероятность каждого из этих элементарных событий одинакова и равна:

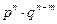
Следовательно, на основании III аксиомы теории вероятности результат равняется:

(сложение вероятностей)

Случайная величина

Пусть имеется вероятностное пространство вида .

Случайной величиной называется измеримая числовая скалярная функция , элементами которой являются элементарные события.

Числовая скалярная функция - это функция, удовлетворяющая следующему условию:

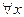событие - алгебре и, следовательно, имеет вероятность наступления.

Если произведено испытание, в результате которого произошло некоторое элементарное событие . В соответствии с функцией этому элементарному событию соответствует число, которое называется реализацией случайной величины x в данном испытании.

В соответствии с определением случайной величины вводится числовая скалярная функция F(x), 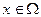, определенная для каждого действительного x и по определению равная вероятности наступления события:

Эта функция называется функцией распределения случайной величины .

Рассмотрим три события:

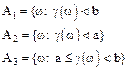
где a<b, a, b - действительные числа.

Свойства:

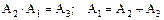
Покажем, что из факта

A₂ Ì s-алгебре

A₁ Ì s-алгебре

и равенства 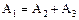следует, что A₃ Ì s.

По определению s-алгебры A₃ измерима, поэтому можно принять III аксиому теории вероятности:

F(x) - неубывающая функция

Если x<y, то

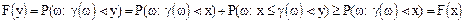
т.к. 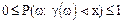, то преобразования верны.

Для всех технических приложений функцию распределения можно считать направленной слева.

В силу того, что функция распределения не убывает, она однозначно задает стчетно-аддитивную меру на поле, порожденном всеми полуинтервалами ненулевой длины.

По введенному полю построим борелевскую алгебру. Обозначим ее b. Возьмем произвольное число BÌb не принадлежащее полю. Это точка или сегмент. Т.к. множество 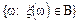получено с помощью счетной суммы или счетного пересечения множеств принадлежащих s-алгебре, то и это множество принадлежит s-алгебре и, следовательно, существует вероятность наступления события B. Следовательно, имеет место следующее эквивалентное определение измеримой функции.

Функция называется измеримой, если для любого BОb множество

алгебре

где

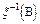множество, полученное следующим образом:

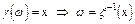
Функция g(x) называется борелевской функцией, если для любого BÌb множество

Борелевская функция - функция, определяемая на системе борелевских множеств.

В функциональном анализе показано, что все известные аналитические функции являются борелевскими.

ТЕОРЕМА:

Пусть g(x) борелевская функция, 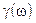- случайная величина, т.е. измеримая функция. Тогда функция

является измеримой и, следовательно, случайной величиной.

Берем произвольное BÌb. 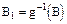по определению борелевской функции.

Рассмотрим множество

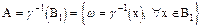
т.к. 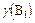измеримая функция и , то AÌs-алгебре

Следовательно, функция - измеримая функция, т.е. случайная величина.

Теорема Колмогорова

Любая числовая скалярная функция, которая удовлетворяет свойствам, которым удовлетворяет функция распределения, является функцией распределения и однозначно задает вероятностное пространство вида:

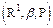
b - борелевская алгебра;

P - мера на борелевской алгебре;

R¹ - числовая скалярная ось.

Введем функцию F(x)

Эта функция определена для всех x, неубывающая, непрерывная сверху. Показать самим, что такая функция однозначно задает счетно-аддитивную меру на поле, порожденном всеми полуинтервалами ненулевой длины.

Докажем, что 0<F(x)<1

Согласно терминологии, если функция y=f(x) непрерывна на отрезке [a, b], то она ограничена. Поскольку наша функция не убывающая, то максимум и минимум она соответственно будет иметь такой:

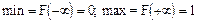
т.е. 0<F(x)<1.

2. Пусть имеем следующие функции.

Построим борелеву алгебру на поле, тогда по теореме о продолжении счетно-аддитивная функция, определенная на поле, без изменения аксиом теории вероятности, однозначно распространяется на все элементы борелевой алгебры, не принадлежащие полю. Т.о. вероятностное пространство построено, теорема доказана.

Смысл теоремы.

Теорема Колмогорова позволяет утверждать, что если вы исследуете случайную величину, то не надо строить абстрактное пространство элементарных событий, s-алгебру, счетно-аддитивную меру, конкретный вид функции 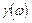. Нашей задачей будет лишь то, что считая R¹ - числовой скалярной осью - пространство элементарных событий, мы должны найти функцию распределения F(x), использую статистику: результата конкретного испытания над случайной величиной:

X₁, X₂,..., X_n

Дискретные случайные величины

Случайная величина называется дискретной, если в результате испытания она может принять значение из конечного либо счетного множества возможных числовых значений.

Случайные величины в дальнейшем будем обозначать большими буквами:

X, Y, Z

Вероятностное пространство дискретной случайной величины задается в виде:

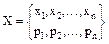, n - конечное или бесконечное.

Пример:

Испытание - композиция n-независимых испытаний, в каждом из которых происходит событие A с вероятностью p, либо 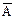с вероятностью 1-p.

Вероятностное пространство

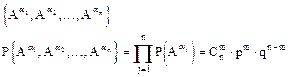
В этом примере s-алгеброй является множество всех подмножеств пространства элементарных событий. Введенную нами случайную величину x по определению можно задать:

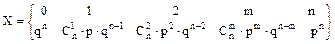
- верхняя строчка - это совокупность возможных числовых значений, которые может принимать случайная величина;

- нижняя строчка - вероятность наступления этих числовых значений.

Практически во всех задачах естествознания отсутствует промежуточный этап: испытание, W - пространство всех возможных исходов испытания, 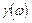- числовая скалярная функция, элементы которой wÌW.

На самом деле структура:

- испытание;

- исход испытания;

- число на числовой оси.

Вероятностные характеристики дискретных случайных величин.

Математическим ожиданием случайной величины X называется число вида

x_i - все возможные различные конкретные исходы испытания;

p_i - вероятности их наступления.

Математическое ожидание является как бы аналогом центра масс точечной механической системы:

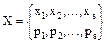
Как центр масс:

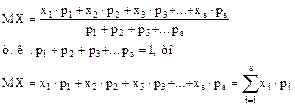
Смысл характеристики мат.ожидания заключается в следующем: это точка на числовой оси, относительно которой группируются результаты конкретных испытаний над дискретной случайной величиной.

Свойства математического ожидания

1. MC=C

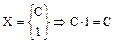
2. MCX=CMX

Построим таблицу для случайной величины CX:

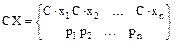
по определению математического ожидания:

3. M(X+a)=MX+a, a=const

Построим таблицу для случайной величины x+a

Доказать следствие

4. M(aX+b)=aMX+b, где a, b - константы

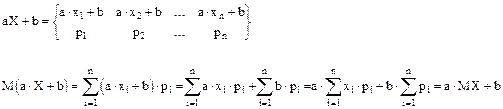
Пусть случайная величина Y является функцией f(x) от случайной величины X. Построим вероятностное пространство случайной величины Y.

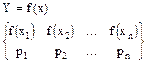
Верхняя строчка является пространством элементарных событий для случайной величины Y. В противном случае верхняя строчка является пространством элементарных событий для величины Y.

Все одинаковые числа в верхней строчке заменяется одним, вероятность наступления которого равна сумме соответствующих вероятностей.

Следствие.

Математическое ожидание случайной величины Y равняется:

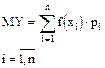
Начальным моментом К-го порядка случайной величины X называется математическое ожидание случайной величины X^k.

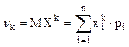
Центрированная случайная величина - это величина, равная X’=X-MX

Покажем, что математическое ожидание MX’ равно 0.

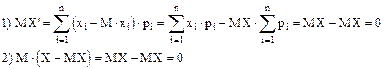
Центральным моментом К-го порядка называется начальный момент К-го порядка случайной величины X’

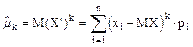
при решении реальных задач практические вероятности р_i неизвестны, но считая, что вероятность - это частость, при большом числе испытаний

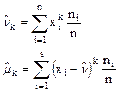
Дисперсией случайной величины X, называется центральный момент второго порядка случайной величины X.

Дисперсия является мерой концентрации результатов конкретных испытаний над случайной величиной X.

Свойства.

1. Чем меньше дисперсия, тем более тесно группируются результаты конкретных испытаний относительно математического ожидания.

Пусть дисперсия мала, тогда мало каждое слагаемое суммы (x_i-n)²p_i. Тогда для, x_i которое по модулю резко отличается от математического ожидания n, p_i - мало. Следовательно, большую вероятность наступления могут иметь лишь те x_i, которые по модулю мало отличаются от математического ожидания.

2. Если дисперсия равна 0, то X - const.

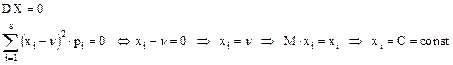
3.

D(X+C)=DX

Y=X+C

Y’=Y-MY=X+C-M(X+C)=X+C-MX-C=X-MX=X’

DY=M(Y’)²=M(X’)²=DX

4.

DCX=C²DX

Y=CX

DY= M(Y’)²=M(Y’)²

Y’=Y-MY=CX-MCX=CX-MCX=C(X-MX)=CX’

DY= M(Y’)²=M(CX’)²=C²M(X’)²=C²DX

5.

Построим функцию распределения для дискретной случайной величины. Для удобства договоримся, что случайные величины располагаются в порядке возрастания.

т.е. по определению для любого действительного X, F(x) численно равно вероятности наступления следующего события: в результате испытаний над X оно приняло значение строго меньше x.

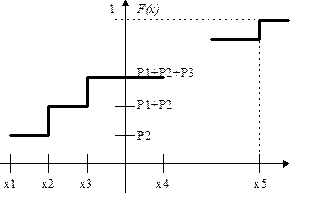
Первая модель распределения Пуассона

Проведена неограниченно большая серия испытаний, в результате каждого испытания случайным образом появляется точка на числовой оси. Случайное распределение точек на числовой оси удовлетворяет следующим трем свойствам.

1. Стационарность. Вероятность того, что на отрезок данной длины попадает данное количество точек определяется только длиной этого отрезка и не зависит от расположения этого отрезка на числовой оси.

2. Ординарность. Вероятность того, что на достаточно малый отрезок длины Dx попадает одна точка, является бесконечно малой Dx порядка. Вероятность того, что на этот отрезок попадает более, чем одна точка, является бесконечно малой более высокого порядка, чем Dx.

3. Свойство без последействия. Вероятность того, что на данный отрезок попало определенное количество точек не зависит от того, сколько точек в результате проведенной бесконечно серии испытаний попало на отрезок, не пересекающийся с данным.

Найти вероятность того, что на данный отрезок длина l попадает m точек.

Обозначим через x^l - случайная величина, равная численности точек, выпавших на отрезок длины l.

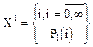
На числовой оси рассмотрим отрезок длины 1 и обозначим:

MX¹=l

Математическое ожидание числа точек, попавших на отрезок длины 1. По свойству стационарности l одинаково для всех отрезков.

MX¹=ll - доказать

Пусть l - целое число. Разобьем отрезок длины l на l отрезков единой длины. Тогда количество точек, попавших на отрезок длины l будет равно числу точек, попавших на каждый из непересекающихся отрезков длины 1 (тут использовалось свойство беспоследействия).

Используя формулу

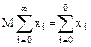
имеем

MX¹=ll

Математическое ожидание числа точек, попавшие на отрезок длины l равно мат. ожиданий точек, попавших на непересекающиеся отрезки. Пусть l - не целое число. Выделяем целую часть. Тогда

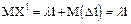
На числовой оси рассмотрим отрезок длины l, разобьем его на n отрезков данной длины

такой, что позволит использовать свойство ординарности. Тогда с определенной погрешностью, которая тем меньше, чем больше n можно считать

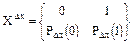
т.е. на отрезок длины Dx попадает не более, чем одна точка, тогда

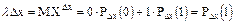
Для достаточного малого отрезка длины lDx вероятность попадания в него одной точки Dx, а вероятность того, что ничего не произойдет 1- lDx.

В сделанных предположениях m точек попадает на отрезок длины l только в одном случае, когда в m отрезках попадает по одной точке. Тогда на основании 3-го свойства искомая вероятность равна

Точную вероятность получим путем предельного перехода при числе разделений отрезка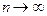

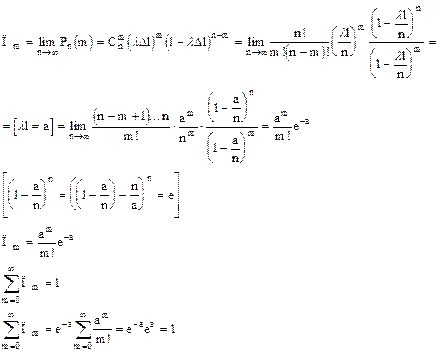
Тут мы разложили в ряд Маклорена.

Найдем производящую функцию распределения Пуассона

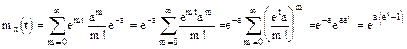
Найти MX и DX

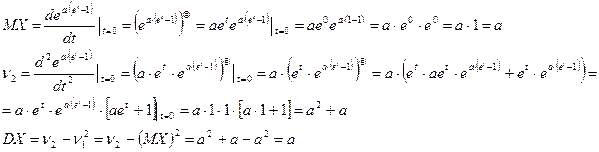
Вторая модель распределения Пуассона

Рассматривается обычная схема биноминального распределения, в котором n - велико, а p - достаточно мало. Тогда точная формула для вероятности появления события A в m испытаниях имеет вид

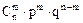
Эта формула при больших n вычисляется сложно. Такую вероятность заменяют приближенной

Для найденного a построим гипотетический ряд вероятностей

Предполагается, что для достаточно больших n и малых p искомая вероятность

является членом построенного гипотетического ряда вероятностей, а во вторых находится в малой окрестности предельного значения этого ряда. И, следовательно, это значение можно взять в качестве допустимой хорошей аппроксимации значений искомой вероятности.

Непрерывные случайные величины.

Будем рассматривать пространство элементарных событий как совокупность всех точек числовой оси. В этом случае введенная ранее функция распределения имеет вид: .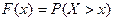

Пусть функция распределения является непрерывной. Найдем вероятность того, что в результате испытаний случайная величина X примет значение a, где a - произвольное действительное число.

P(X=a).

Рассмотрим неравенство:

Доказать самим.

Следовательно:

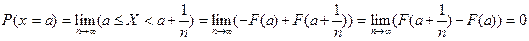
Мы впервые столкнулись с ситуацией, когда событие принципиально может произойти в результате испытания, но имеет вероятность равную 0. В инженерном толковании это означает: в данной конечной серии испытаний данное событие никогда не произойдет.

Случайная величина X называется непрерывной, если ее пространством элементарных событий является вся числовая ось (либо отрезок (отрезки) числовой оси), а вероятность наступления любого элементарного события равна нулю.

P(a£X<b)=P(a£X£b)=F(b)-F(a)

Если от сложного события вычесть конечное либо счетное множество, вероятность наступления нового события останется неизменной.

Функция f(x) - числовая скалярная функция действительного аргумента x называется плотностью вероятности, и существует в точке x, если в этой точке существует предел:

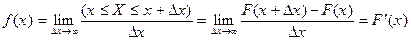
Свойства плотности вероятности.

1. Плотность вероятности является неотрицательной функцией.

2.

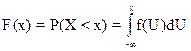
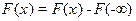
3.

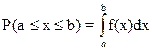
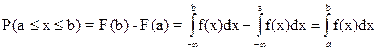
4.

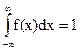
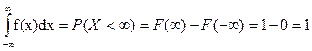
Следствие: Если пространством элементарных событий является отрезок числовой оси, то пространство элементарных событий формально можно распространить на всю числовую ось, положив вне отрезка значение плотности вероятности равное 0.

Вероятностные характеристики непрерывных случайных величин.

Пусть имеется случайная величина, являющаяся функцией от непрерывной случайной величины X.

Y=x(x)

Математическим ожиданием непрерывной случайной величены является число:

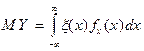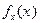, - плотность вероятности случайной величины.

Обоснование этой формулы.

Аппроксимируем непрерывную случайную величину Y случайной величены Y^*, которая является дискретной. Пусть числовая ось - пространство элементарных событий случайной величены X, разобьем всю числовую ось на отрезки достаточно малой длины.

2n отрезков.

Если в результате испытания случайная величена X попала в отрезок с начальной вершиной x_i, то случайная величена X^* приняла значение x(x_i) с точностью до бесконечно малой Dx - длины i-го отрезка. Вероятность того, что Y^* примет значение x(x_i) с точностью до бесконечно малой более высокого порядка, чем Dx, тем более точно Y^* аппроксимирует Y.

Вероятность наступления x(x_i) для Y^* равна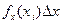

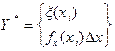
, при эта сумма переходит в .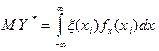

Тогда .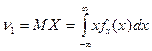

Самим показать, что все свойства мат. ожидания для дискретной случайной величены сохраняются для непрерывной случайной величены.

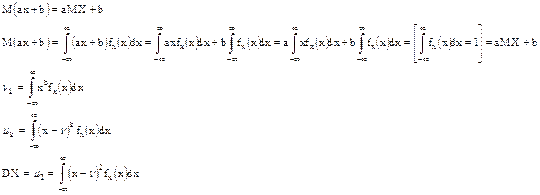
Доказать, что

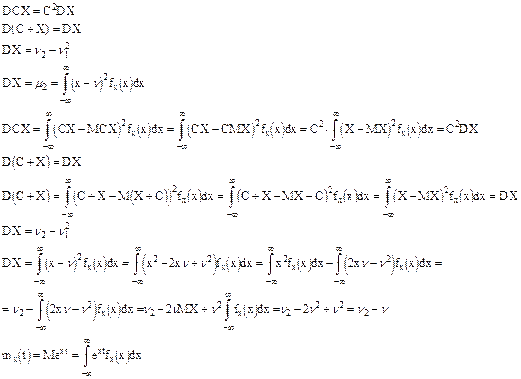
Доказать самим, что свойство 1 и 2 для производящей функции в дискретном случае справедливы и для непрерывного.

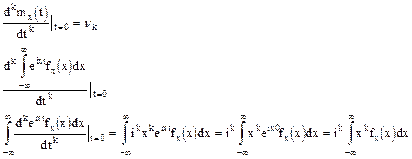
Неравенство Чебышева

Рассмотрим случайную величину X с конечным мат. ожиданием и дисперсией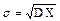

Для любого неотрицательного числа t вероятность наступления события

Пусть Z - непрерывная случайная величина с плотностью вероятности f(Z). Пространство событий величины Z (0; ¥). Тогда имеет место неравенство

Доказать неравенства

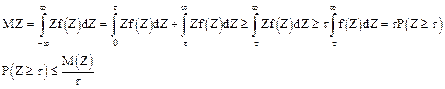
Рассмотрим два сложных события

a - произвольное действительное число.

Показать самим, что x - удовлетворяет и одному и другому неравенству.

Тогда 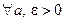справедливо

В данном случае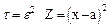

Равномерность неравенств при e>0

или, в частности, при a=n=MX

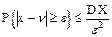
при e=st справедливо неравенство Чебышева.

Дата добавления: 2014-01-14