Равновесия в системе жидкость - жидкость

Для трехкомпонентной системы жидкость – распределяемое вещество–жидкость можно изменять концентрацию одной из фаз без нарушения равновесия. В процессе жидкостной экстракции обычно Т не меняется, Р на равновесие системы не влияет.

Закон распределения: отношение равновесных концентраций распределяемого между двумя жидкими фазами вещества при Т=const есть величина постоянная.

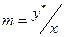или 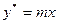(5.141)

где у* и х – равновесные концентрации распределяемого вещества соответственно в экстракте и рафинате, m – коэффициент распределения.

По формуле (5.141) линия равновесия должна быть прямой, выходящей из начала координат. Однако это справедливо для случая полной взаимной нерастворимости участвующих в процессе фаз, что довольно редко встречается в реальных условиях. Обычно m зависит от концентрации распределяемого вещества Т=const, если же меняется Т, то величина m может меняться еще сильнее.

Линии равновесия на диаграмме у-х при постоянной темпиратупе называют изотермами экстракции (рис. 5.48). Если известны изотермы для разных Т, то становится возможным выбрать наиболее приемлемое Т.

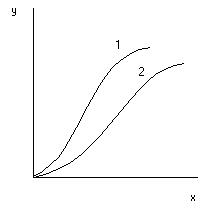1 – неэлектролит

2 – электролит

Рис.5.48 Типичные изотермы экстракции.

Треугольные диаграммы. Отметим, что часто фазы, участвующие в процессе экстракции, частично растворимы друг в друге. Тогда экстракт помимо экстрагента и растворенного вещества содержит некоторое количество растворителя из исходного раствора, а рафинат помимо первоначального раствора и некоторого количества растворенного вещества – определенное количество экстрагента. Оба раствора состоят из трех компонентов.

А, В, С – чистые компоненты. В точке А – чистый Фх, в точке 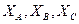В – чистый М, в точке С – чистый Фу. Точка М характеризуется величинами. Точки на площади треугольника соответствуют составам трехкомпонентных растворов.

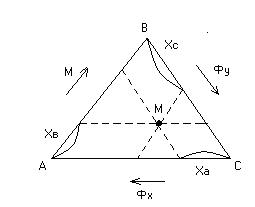
Рис. 5.49 Треугольная диаграмма

Равновесную концентрацию для трехкомпонентных смесей ж-ж можно представить на треугольной диаграмме.

Рис. 5.50 Равновесная кривая в треугольной диаграмме.

А – 100% - растворитель в исходном растворе,

В – 100% - растворенное вещество,

С – 100% - экстрагент

Линии АВ, ВС, СА – характеризуют состав двухкомпонентных растворов. Пусть А и В, В и С, неограниченно растворимы друг в друге, а А и С – ограниченно растворимы. Пусть состав А и С характеризуются точками G₁ и G₂. Если к ним добавить В, получим трехкомпонентный расслаивающий раствор соответствующий точкам D₁ и D₂. Эта хорда соответствует растворам, находящихся в равновесии друг с другом. Точка К – критическая точка, соответствует однофазному раствору.

Взаимная растворимость с увеличением температуры повышается, поэтому область существования гетерогенных систем уменьшается. При высоких температурах может вообще исчезнуть (точка Т_кр на рис. 5.51).

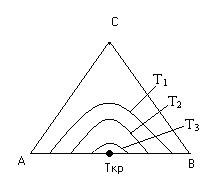
Рис. 5.51 Влияние Т на равновесную кривую.

Селективность экстрагента. Основным свойством экстрагента является селективность, которая характеризует его способность преимущественно извлекать один из двух, трех и более компонентов раствора. Селективность экстрагирования по отношению к распределяемому компоненту характеризуется коэффициентом селективности (коэффициент разделения)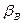

(5.142)

или с учетом (5.141)

(5.143)

Как видно, чем больше 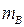тем больше 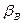. Если 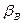=1, то селективность равна 0. В реальных условиях 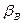больше 2.

Обозначены через у – экстракт, х – рафинат.

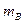- коэффициент распределения для компонента В.

5.4.1.2 Материальный баланс процесса жидкостной экстракции

Однократная (одноступенчатая) экстракция.

Рассмотрим одноступенчатую (однократную) экстракцию. Этот простейший метод заключается в том, что исходный раствор F и экстрагент S перемешивается в смесителе, после чего разделяется на два слоя: экстракт E и рафинат R.

F + S = E + R (5.144)

Рис. 5.52 Схема одноступенчатой экстракции.

Фазы, участвующие в жидкостной экстракции, обладают частичной взаимной растворимостью. Тогда система как минимум является трехкомпонентной. Для трехкомпонентной смеси используется треугольная диаграмма. Уравнение (5.144) можно переписать (при разделении N кг исходной смеси).

F + S = N = R + E (5.145)

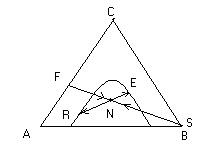
Рис. 5.53 К выводу уравнения материального баланса.

Выражение (5.145) позволяет представить материальный баланс на треугольной диаграмме как процесс смешения потоков F + S = N и затем разделения этой тройной смеси состава N на потоки R + E. По правилу рычага можно записать

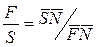(5.146)

Точки при заданной F находим необходимое значение S для процесса. Соотношение потоков Е и R находят по формуле

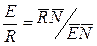(5.147)

Материальный баланс компонентов А и В в потоках экстракта Е и рафината R с учетом (5.142) имеет вид:

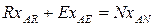(5.148)

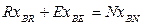(5.149)

Так как сумма концентраций всех трех компонентов А, В, С равна 100%, то матбаланс по компоненту С не нужен. Учитывая, что N = E + R получим:

Разделив одно на другое получим:

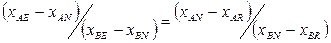(5.150)

Уравнение (5.150) является уравнением прямой линии. По уравнениям (5.144) и (5.150) можно найти состав любого потока, если известны количества и состав трех остальных потоков.

В соответствии с общим уравнением массопередачи количество проходящего из одной фазы в другую вещества М можно записать:

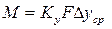
(5.151)

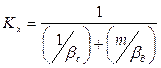
Здесь 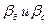- коэффициенты массоотдачи для дисперсной фазы и сплошной фазы.

Поскольку поверхностью контакта фаз при экстракции является капли, то массоперенос осуществляется через сферическую поверхность. Очевидно, что гидродинамические условия внутри капли и в сплошной фазе различны. Поэтому массоперенос в пределах каждой из фаз не может быть описан идентичным уравнением.

5.4.1.3 Основные способы проведения экстракции

Однократная (одноступенчатая) экстракция.

Многоступенчатая экстракция с перекрестным током растворителя. Исходный раствор и соответствующие рафинаты обрабатывают порцией свежего экстрагента S1 и S2 и т. д. На каждой ступени экстракции, состоящей из смесителя и отстойника, причем рафинаты направляют последовательно в следующие ступени, а экстракты Е1 и Е2 и т. д. после каждой ступени выходят из колонны.

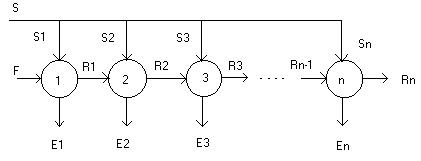
Рис. 5.54 Схема многократной экстракции с противоточным током растворителя.

По этому способу можно полностью извлечь из исходного раствора распределяемый компонент и получить чистый рафинат. Однако, неизбежны потери растворителя, содержащегося в исходном растворе, так как в каждой ступени происходит частичное удаление растворителя экстрактом.

Многократная экстракция с противоточным движением растворителя.

Этот способ проведения экстрагирования характеризуется многократным контактированием ступени 1, 2 и т. д. при противоточном движении потоков рафината R и экстракта Е при условии подачи исходного раствора F и и экстагента S с противоположных концов.

Рис. 5.55 Схема многократной экстракции с противоположным движением растворителя.

Непрерывная противоточная экстракция. Такой способ экстрагирования осуществляют в аппаратах колонного типа (например, насадочных). Более тяжелый раствор поступает сверху, в нижнюю часть колонны поступает легкая фаза.

5.4.2 Экстрагирование в системе твердое тело – жидкость (выщелачивание).

Экстрагированием называется процесс извлечения одного или нескольких компонентов из твердого материала путем избирательного растворения в жидкостях (экстрагентах). Извлекаемые материалы содержатся в порах твердого тела в виде растворенного вещества или в виде твердой фазы. В первом случае говорят об экстрагировании растворенного вещества, во вторым – об экстрагировании твердого вещества.

Экстрагирование растворенного вещества: растворенное вещество, содержащейся в пористой структуре твердого тела, диффундирует в основную массу жидкости, концентрация целевого компонента в порах снижается, а в жидкости (экстрагенте) увеличивается. Организация процесса по противотоку позволяет достигать высоких степеней извлечения.

Механизм экстрагирования твердого тела:

- проникание экстрагента в пористую структуру твердого тела;

- растворение целевого компонента в экстрагенте;

- диффузия растворенного компонента в основную массу жидкости.

Чаще всего процесс лимитируется третьей стадией, как наиболее медленной. Перенос вещества к границам пористого тела происходит с помощью механизма молекулярной диффузии в неподвижной жидкости, заполняющей пористый объем.

5.4.2.1 Экстрагирование растворенного вещества.

Твердое тело содержит в своем пористом объеме раствор целевого компонента. Диаметр пор, составляющих пористый объем, настолько мал, что жидкость, заключенная в порах, практически неподвижна. Из этого следует, что механизмом переноса растворенного вещества является молекулярная диффузия.

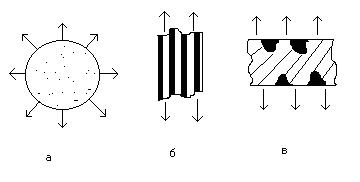
Рис. 5.56 Варианты строения пористых тел: а – изотропное пористое тело, б – анизотропное пористое тело с регулярной структурой, в – анизотропное пористое тело с нерегулярной структурой.

Молекулярный перенос завершается по достижении целевым компонентом внешних границ пористого тела, после чего реализуется конвективный перенос вещества в жидкой среде, окружающей пористое тело. Имеем трехкомпонентную систему:

- А – нерастворимое вещество, а порах которого находится В.

- В – экстрагируемое вещество.

- С – экстрагент.

Для трехкомпонентной системы связь между ее составом удобно представлять в треугольной системе координат.

Рис. 4.57 Треугольная диаграмма для системы твердая фаза – жидкость.

А, В, С – соответствующие компоненты. АВ, ВС, АС – бинарные смеси этих компонентов – А + В, В + С, А + С. Точки внутри треугольника отражают состав тройных смесей.

При условии, что точка Е соответствует насыщенному состоянию экстракта (В + С) при данной температуре, область АЕС диаграммы отвечает насыщенному состоянию раствора компонентов В и С.

Тогда возможен переход В из твердой фазы в жидкую. Составы и количества образующихся смесей определяется по правилу рычага.

Рассмотрим сферическое твердое тело, в пористом объеме которого содержится раствор целевого компонента с первоначальной концентрацией Сн. Поле концентрации внутри пористого тела может быть описано уравнением:

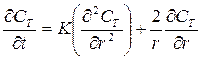(5.152)

Граничные условия:

при t = 0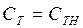

при r = 0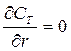

при r = R (5.153)

Здесь 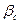- коэффициент массоотдачи, Сп – концентрация на поверхности r = R, К – коэффициент массопроводности (эффективной диффузии). К зависит от природы пористого тела, его структуры, свойства жидкости и концентрации переносимого вещества. Система (5.152) – (5.153) имеет решение. Однако, анализ ситуации ведут по критерию Био.

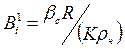(5.154)

По форме критерия Био аналогичен критерий Nu. Однако, если Nu для одной фазы, то Био содержит коэффициент массотдачи жидкой фазы β_с и коэффициент эффективной диффузии для твердой фазы.

При (на практике 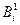>20) процесс лимитируется внутренней диффузией

При 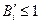– внешнее диффузионное сопротивление начинает доминировать.

5.4.2.2 Экстрагирование твердого вещества.

Извлекаемое вещество распределено равномерно по объему сферы.

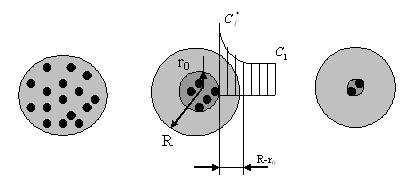
Рис.5.58 Изменение структуры в пористой частице в процессе экстрагирования твердого вещества.

Процесс описывается уравнением (5.152)

Граничные условия другие

При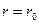

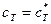
При 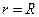(5.155)

Однако процесс этот крайне медленный, поэтому реализуется стационарное распределение концентраций то есть можно принимать

Тогда решение имеет вид:

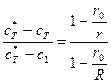(5.156)

Время полного экстрагирования твердого вещества определяется при 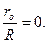В уравнении (5.156) времени нет.

Введем еще одно уравнение.

Извлекаемое вещество сосредоточено в объеме 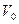. Изменение массосодержания в объеме V равна приходу массы из 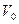и уходу массы с наружной поверхности :

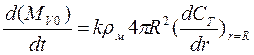(5.157)

После решения (5.157) с учетом (5.156) дает:

(5.158)

Здесь 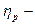плотность распределения (масса извлекаемого вещества в единице объема частицы).

Дата добавления: 2014-01-14