Степенные ряды. Простейшим примером функционального ряда является степенной ряд – ряд вида

Простейшим примером функционального ряда является степенной ряд – ряд вида 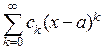. Числа 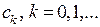, называются коэффициентами степенного ряда. Поскольку простой заменой переменной исходный степенной ряд превращается в ряд 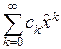, мы будем рассматривать только степенные ряды вида 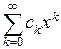. Очевидно, что такой ряд обязательно сходится в точке 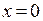. Ответом на вопрос об области сходимости степенного ряда дает

Теорема Абеля. Пусть ряд 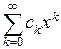сходится в точке 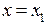, тогда он сходится, причем абсолютно, при .

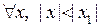Пусть ряд 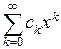расходится в точке 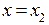, тогда он расходится при .

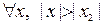Доказательство. Так как ряд 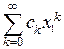сходится, то общий член этого ряда стремится к нулю, и значит, ограничен, то есть, 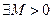тчо .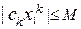

Пусть 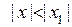тогда 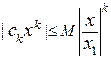. Так как ряд 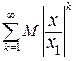сходится, то по теореме сравнения абсолютно сходится ряд .

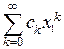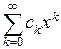Так как расходится, то не может сходиться ни при каких значениях 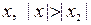, так как в противном случае он бы сходился, в

соответствии с доказанной частью теоремы, и при .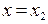

Из теоремы Абеля следует, в частности, что область сходимости степенного ряда 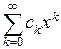представляет собой некоторый интервал 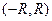, а область расходимости – внешность этого интервала. Что касается двух точек 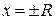, являющихся границами этого интервала, то сходимость или расходимость ряда в этих точках следует проверять для каждой функции индивидуально.

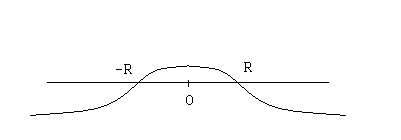
Число 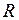называется радиусом сходимости степенного ряда. Интервал 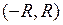называется интервалом сходимости степенного ряда.

Дата добавления: 2014-01-14