Гармонический осциллятор

Законы сохранения импульса и энер­гии определяются как следствия однородности пространства и времени.

Векторная сумма моментов импульса всех частиц замкнутой системы остается постоянной.

Закон сохранения суммарного момента импульса универсален, верен для любой замкнутой системы тел.

ЧЕТЫРЕ ОСНОВНЫХ ТИПА ВЗАИМОДЕЙСТВИЙ В ПРИРОДЕ

Обнаружены лишь четыре типа взаимодействий, которые лежат в основе всех сил и взаимодействий во Вселенной.

ВЗАИМОДЕЙСТВИЕ	ИСТОЧНИК	ОТНОСИТ. ИНТЕНСИВНОСТЬ	РАДИУС ДЕЙСТВИЯ
Гравитационное	Масса	10^-^38	Дальнодействующее
Слабое	Элементарные частицы	10^-15	Короткодействующее 10^-15 м.
Электромагнитное	Электрические заряды	10^-^2	Дальнодействующее
Ядерное (сильное)	Адроны (протоны, нейтроны, мезоны)		Короткодействующее 10^-15 м

Колебания и волны в природе и их описание.

Колебания и волны в природе наблюдаются какволнение и зыбь в озерах, прудах и океанах; волны землетрясений, изучаемые сейсмологами; элект­ромагнитные волны, которые образуют свет и передают инфор­мацию по теле- и радиоканалам; волны вероятности, используе­мые в мире квантов для предсказания поведения микрочастиц и более сложных форм вещества.

Механические колебания — это движения, которые повторяют­ся через определенные промежутки времени. Чаще всего они возни­кают при нарушении устойчивого состояния равновесия системы, при этом равнодействующая сил не равна нулю.

Одна из сил долж­на зависеть от времени, и система должна обладать избыточной энергией.

Колебания могут происходить при наличии упругих сил, силы тяжести; электричес­кие колебания (напряжений и сил токов) происходят в электри­ческих цепях, а вокруг этих цепей колеблются напряженности элек­трического и магнитного полей.

Несмотря на разную природу коле­баний, в них обнаруживаются общие закономерности.

Физическая система, совершающая колебания, называется осциллятором.

Гармонический осциллятор, определяемый колебаниями мас­сы, прикрепленной одним концом к пружине, является самым простым примером гармонического движения. Математический маятник состоит из точечной массы, подвешенной на невесомой и нерастяжимой нити.

При малой амплитуде почти каждый коле­бательный процесс можно считать гармоническим (рис. 3.3).

Период колебаний маятника при малых амплитудах, как установил еще Галилей, определяется его длиной и не зависит от массы маятника.

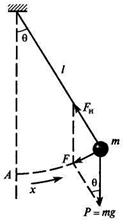
Рис. 3.3. Модель ма­тематического маят­ника

Период колебания маятников разной длины l про­порционален квадратному корню из их длин

;

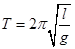пружины — обратно пропорционален собственной частоте колебаний

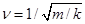
(k — жесткость пружины).

Это свойство изохронности колебаний маятника использовалось в XVII в. для отсчета равных промежутков времени, но колеба­ния затухали, приходилось маятник подталкивать, и не было автоматического счета числа колеба­ний.

Гюйгенс применил маятник в своих часах в качестве регулятора и довел их до практического использования и коммерческого успеха. Восемнад­цатое столетие даже получило наименование века часов, хотя тогда они использовались, в основ­ном, для определения долготы места.

РАЗВЕРТКА КОЛЕБАНИЙ

Прикрепим к нижней части грузила маятника мяг­кий грифелек и подвесим маятник над листом бумаги так, чтобы грифель касался бумаги (рис. 4.3). Теперь слегка отклоним маятник. Качающийся грифелек про­чертит на бумаге небольшой отрезок прямой линии. В середине качания, когда маятник проходит положе­ние равновесия, карандашная линия будет пожирнее, так как в этом положении грифелек сильнее нажимает на бумагу. Если потянуть лист бумаги в направлении, перпендикулярном к плоскости колебания, то прочер­тится кривая, изображенная на рис. 4.3.

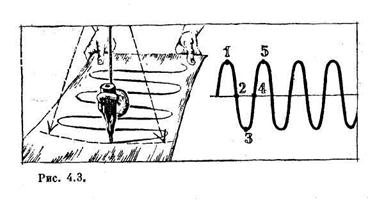
Нетрудно сообразить, что получившиеся волны будут распо­ложены густо, если бумагу тянуть медленно, и редко, если лист бумаги движется со значительной скоростью. Чтобы кривая получилась аккуратной, как на рисунке, нужно, чтобы лист бумаги двигался строго равномерно.

Этим способом мы как бы «развернули» колебания.

Развертывание нужно для того, чтобы сказать, где находился и куда двигался грузик маятника в тот или иной момент времени. Представьте себе, что бумага дви­жется со скоростью 1 см/с с момента, когда маятник находился в крайнем положении, например слева от средней точки. На нашем графике это начальное поло­жение соответствует точке, помеченной цифрой 1. Через ¹/₄ периода маятник будет проходить через среднюю точку. За это время бумага продвинется на число сантиметров, равное-¹/₄ Т, — точка 2 на рисунке.

Теперь маятник движется вправо, одновременно ползет и бумага. Когда маятник придет в правое крайнее положение, бумага продвинется на число сантиметров, равное ¹/₂ Т, —точка 3 на рисунке. Маятник вновь идет к средней точке и попадает через ³/₄ Т в положение

равновесия — точка 4 на чертеже. Точка 5 завершает полное колебание, и дальше явление повторяется через каждые Т секунд или через каждые Т сантиметров на графике.

Таким образом, вертикальная линия на графике — это шкала смещений точки от положения равнове­сия, горизонтальная средняя линия — это шкала вре­мени.

Из такого графика легко находятся две величины, исчерпывающим образом характеризующие колебание.

Период определяется как расстояние между двумя равнозначными точками, например между двумя бли­жайшими вершинами.

Наи­большее смещение точки от положения равновесия называется амплитудой колебания.

Кривая зависимости смещения от времени представляет собой синусоиду.

Если смещение точки обозначить через у, амплитуду через a,

период колебания через Т, то значение смещения через время t после начала колебания найдем по формуле

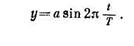
Колебание, происходя­щее по такому закону, на­зывается гармоническим.

Аргумент синуса равен произведению 2на t/T. Величина 2 t/T называет­ся фазой.

Волновое описание процессов. Типы и свойства волн.

Поперечные и продольные волны

В поперечных волнах частицы перемещаются перпенди­кулярно направлению распространения волны.

В электромагнитных волнах направления электрического и магнитного полей перпен­дикулярны направлению распространения волны.

В продольных волнах частицы перемещаются вдоль направления распространения волны, например, распростра­нение звука в воздухе или волн сжатия —растяжения в самой пру­жине. В звуковых волнах плотность газа, где распространяется зву­ковая волна, меняется по закону синуса.

Свет.

Дисперсией называется зависимость показателя преломления п света от частоты колебаний v (или длины волны ).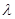

Ньютон отме­тил, что разложение белого света в спектр — проявление диспер­сии.

Таким образом, в одном и том же веществе ско­рости света для разных частот различны, различны и показатели преломления п, причем п зависит от v.

Явление дифракции (от лат. diffractus — разломанный) возника­ет, если плоская волна длиной волны 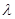попадает на преграду со щелью шириной s, причем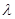 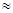s.

Монохроматическая электромагнитная волна, распространяю­щаяся вдоль х, представляет собой электромагнитное поле. Волны изображаются (рис. 2.6) так, что вектор Е и вектор H одновременно достигают максимума и мини­мума, т. е. находятся в фазе, и энергия течет вдоль х (вектор v).

Рис. 2.6. Векторы Е и Н в бегущей волне находятся в фазе.

Поляризованный и неполяризованный свет

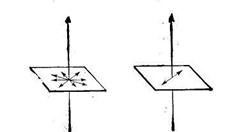
РИС. Колебания в неполяризованном и поляризованном свете.

Дата добавления: 2014-01-14