
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
В итоге получается
|
|
|
|
С помощью этих кодов упрощается операция алгебраического сложения (вычитания). Она сводится к операции простого сложения, что не вызывает затруднения. Применение кодов упрощает определение знака результата, и признака переполнения разрядной сетки.
Как видно из примеров, все операции с двоичными числами сводятся в конечном итоге к сложению и вычитанию. Если сложение чисел с одинаковыми знаками не вызывает затруднения, то операция сложения чисел с различными знаками (вычитание) требует дополнительных действий. В этом случае требуется определять большее по модулю число, затем определять его знак, чтобы потом его использовать как знак результата, вычитать из числа с большим модулем число с меньшим модулем. Это упрощается, если использовать методы, которые сводятся к представлению чисел в виде специальных кодов. Различают три вида кодов
- прямой,
- обратный,
- дополнительный.
Для обозначения знака числа в каждом из перечисленных кодов выделяется специальный знаковый разряд. Он всегда представляется первым слева от цифровых разрядов в разрядной сетке и играет роль старшего разряда числа. Если число положительное, то в этом (знаковом) разряде записывается нуль, если число отрицательное, то в нем записывается единица.
П р я м о й к о д
Прямой код 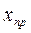 двоичного числа
двоичного числа 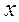 содержит цифровые разряды, слева от которых записывается знаковый разряд, который выполняет не роль з н а к а, а роль значущей цифры числа. Например, целое положительное двоичное число х=+ 11010 в прямом коде будет иметь вид
содержит цифровые разряды, слева от которых записывается знаковый разряд, который выполняет не роль з н а к а, а роль значущей цифры числа. Например, целое положительное двоичное число х=+ 11010 в прямом коде будет иметь вид  = 011010, а отрицательное число у= - 10011 будет иметь вид
= 011010, а отрицательное число у= - 10011 будет иметь вид 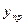 = 110011. В этих кодах знаковые разряды выполняют роль значащих цифр.
= 110011. В этих кодах знаковые разряды выполняют роль значащих цифр.
О б р а т н ы й к о д
Обратный код образуется из прямого кода путем замены единиц и нулей в цифровых разрядах на их противоположные значения, то есть единицы заменяются нулями, а нули – единицами. Например, число
у= -10011 имеет прямой код 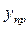 = 110011, то его обратный код будет иметь вид
= 110011, то его обратный код будет иметь вид  =101100. Здесь знаковый разряд не меняет своего значения, а цифровые разряды заменены противоположными значениями.
=101100. Здесь знаковый разряд не меняет своего значения, а цифровые разряды заменены противоположными значениями.
Д о п о л н и т е л ь н ы й к о д
Дополнительный код получается из обратного путем прибавления единицы к младшему разряду.
То есть, если обратный код числа у= -10011 представляет собой
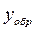 = 101100,
= 101100,
то дополнительный код будет иметь вид
 101100
101100
+
1
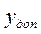 101101
101101
Использование обратного и дополнительного кода позволяет значительно упростить процесс алгебраического сложения (вычитания) и свести его к простому арифметическому сложению. В этом случае положительное число представляется всегда только в прямом коде, а отрицательное число – либо в обратном, либо в дополнительном коде. Затем производится арифметическое сложение этих кодов, включая и знаковые разряды, воспринимаемые как старшие. В этом случае выполняются следующие правила:
- при использовании обратного кода, возникающая единица переноса из знакового разряда прибавляется к младшему разряду суммы,
- при использовании дополнительного кода, возникающая единица переноса отбрасывается.
Например, требуется сложить два числа х = 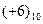 =
= 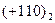 и у=
и у= .
.
Прямой код для положительного числа х имеет вид
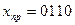
Прямой код для отрицательного числа у

Обратный код для отрицательного числа у
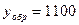
Дополнительный код для отрицательного числа у
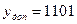
Операция сложения с использованием обратного кода отрицательного числа у.
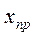 0110
0110
+
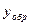 1100
1100

 +
+
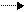 1 перенос единицы со знакового разряда с добавлением в младший разряд суммы.
1 перенос единицы со знакового разряда с добавлением в младший разряд суммы.
В результате получается
х + у = 0011 =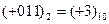
Операция сложения с использованием дополнительного кода
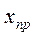 0110
0110
+
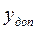 1101
1101
1 0011

 отбрасывание
отбрасывание
х + у = 0011= 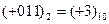 .
.
Это отвечает истинному результату алгебраического сложения 6 – 3 = 3.
Следует отметить, что если результат сложения положительный
(нуль в знаковом разряде), то он воспринимается как прямой код. Если же результат сложения отрицательный (единица в знаковом разряде), то он воспринимается в том коде, в каком было представлено отрицательное число при сложении. Например, необходимо сложить два числа х= и у=
и у=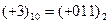 . Прямой, обратный и дополнительный код отрицательного
. Прямой, обратный и дополнительный код отрицательного
числа х имеют вид соответственно 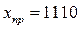 ,
, 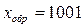 и
и 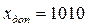 . Положительное число у используется только в прямом коде
. Положительное число у используется только в прямом коде  . Алгебраическое сложение с использованием обратного кода отрицательного числа х
. Алгебраическое сложение с использованием обратного кода отрицательного числа х
1001
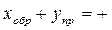
0011
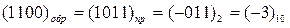 .
.
Здесь полученный результат отрицательный, о чем свидетельствует единица в знаковом разряде. Коль скоро он отрицательный, то его код воспринимается как код отрицательного слагаемого х, то есть обратный. Чтобы перевести результат в обратном коде в десятичную систему счисления, необходимо обратный код перевести в прямой, затем в двоичный, а потом в десятичный код.
Алгебраическое сложение с использованием дополнительного кода отрицательного числа х.
1010
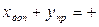
0011
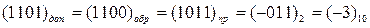
Здесь отрицательное слагаемое х использовано в дополнительном коде, поэтому и результат воспринимается в дополнительном коде. Путь перевода результата в десятичную систему счисления аналогичен предыдущему случаю.
Следует иметь в виду, что для заданной длины разрядной сетки, дополнительным кодом представляется на единицу больше отрицательных чисел, чем положительных. Например, в 8-разрядной сетке можно представить наибольшее положительное число +127 в прямом коде как 01111111 и наименьшее отрицательное число –128 в дополнительном коде как 10000000. По этим причинам для представления отрицательных чисел в компьютере чаще используется дополнительный код.
Операция алгебраического сложения чисел, представленных
в форме с фиксированной точкой
При алгебраическом сложении чисел, представленных в форме с фиксированной точкой, слагаемые представляются в дополнительном коде, так как они хранятся в памяти в этом коде. Если результат положительный (нуль в знаковом разряде), то он воспринимается в прямом коде (для положительных чисел прямой и дополнительный код одинаков), если результат отрицательный (единица в знаковом разряде), то он воспринимается в дополнительном коде.
Иногда при сложении кодов возникает переполнение разрядной сетки, что ведет к искажению результата. Переполнение устанавливается путем анализа переносов в знаковый разряд и из него. Признаком переполнения является наличие переноса в знаковый разряд суммы при отсутствии переноса из знакового разряда (положительное переполнение) или наличие переноса из знакового разряда суммы при отсутствии переноса в ее знаковый разряд (отрицательное переполнение). При положительном переполнении – результат операции положительный, а при отрицательном – отрицательный.
Если же переносов из знакового разряда и в знаковый разряд суммы нет или есть оба эти переноса, то переполнения нет и при нуле в знаковом разряде сумма положительная и представлена в прямом коде, а при единице в знаковом разряде сумма отрицательная и представлена в дополнительном коде.
Операция алгебраического сложения чисел представленных
в форме с плавающей точкой
Начинается операция с выравнивания порядков слагаемых. При этом порядок меньшего по модулю числа принимается равным порядку большего по модулю числа, а его мантисса сдвигается вправо на число шестнадцатиричных разрядов равное разности порядков.
В процессе сдвига мантиссы меньшего слагаемого происходит потеря младших разрядов, что вносит погрешность в результат операции. При этом может оказаться, что мантисса меньшего слагаемого сдвигается за пределы разрядной сетки. Тогда в качестве суммы принимается большее по модулю слагаемое.
После выравнивания порядков начинается алгебраическое сложение мантисс по таким правилам, как и для чисел с фиксированной точкой. Порядок результата принимается равным порядку большего слагаемого. Если в процессе суммирования условие 1/16 <= /m/ <1 не выполняется, то это может привести к нарушению нормализации мантиссы m. В этом случае производится сдвиг мантиссы с соответствующим изменением порядка результата.
Операции сложения чисел, представленных в форме с плавающей точкой, требуют большего времени, чем операции с числами, представленными в форме с фиксированной точкой.
Принципы аппаратной реализации операций умножения
и деления
Операция умножения двоичных целых чисел, представленных в форме с фиксированной точкой, приводит к формированию в АЛУ компьютера произведения, имеющего двойную длину по сравнению с множителями.
Для реализации умножения необходимо иметь регистры множимого и множителя, а также сумматор, в котором производится последовательное суммирование частных произведений. Для (n-1) – разрядных сомножителей операция умножения состоит из (n-1) циклов. В каждом цикле инициализируется очередная цифра множителя. Если это единица, то к содержимому сумматора частичных произведений добавляется множимое, в противном случае (очередная цифра нуль) прибавление не производится. При этом множитель и сумма частичных произведений сдвигаются на один разряд вправо относительно неподвижного множителя.
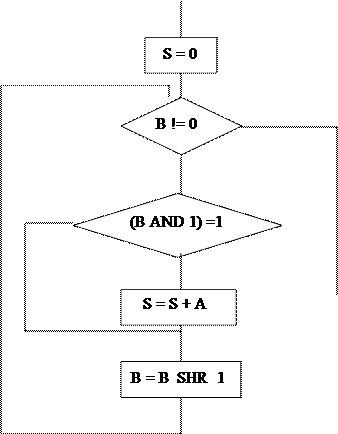
Поскольку, по мере сдвига множителя, старшие разряды регистра множителя освобождаются, они могут быть использованы для хранения младших разрядов произведения, поступающих из сумматора частных произведений в процессе выполнения умножения. Для этого младший разряд сумматора частичных произведений соединяется со старшим разрядом регистра множителя. После завершения операции умножения старшие разряды произведения находятся в регистре сумматора, а младшие – в регистре множителя. На рис. 6.3 приведен алгоритм умножения чисел А и В.
Здесь логическая операция AND с константой 1 позволяет выделить младший разряд множителя с целью формирования определенного частичного произведения. SHR – сдвиг множителя на один разряд вправо.
Правило перемножения целых двоичных чисел очень похоже на перемножение в столбик. Пусть заданы множимое А=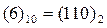 и множитель В=
и множитель В=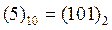 . Перемножение их по известным правилам арифметики имеет вид
. Перемножение их по известным правилам арифметики имеет вид
1 1 0
*
1 0 1
1 1 0
+ 0 0 0
1 1 0
 1 1 1 1 0
1 1 1 1 0

+

+

Рис. 6.2 Алгоритм умножения чисел А и В
Поскольку 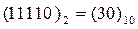 полученный результат является верным. Для выполнения этой операции в компьютере используются трехразрядные регистры множимого, множителя и сумматора частичных произведений. Сдвиг множимого А и суммы частичных произведений S производится вправо. По мере выполнения операций умножения младшие разряды суммы частичных произведений S перемещаются в старшие (освобождающие) разряды регистра множителя. Последовательность операций имеет следующий вид, представленный в таблице
полученный результат является верным. Для выполнения этой операции в компьютере используются трехразрядные регистры множимого, множителя и сумматора частичных произведений. Сдвиг множимого А и суммы частичных произведений S производится вправо. По мере выполнения операций умножения младшие разряды суммы частичных произведений S перемещаются в старшие (освобождающие) разряды регистра множителя. Последовательность операций имеет следующий вид, представленный в таблице
| Операции | Разряд множителя В | Реализация |
| S – 0 | 0 0 0 + 1 1 0 | |
| S = S + A | ||
| S | 1 1 0 | |
| SHR 1 | 0 1 1 0 | |
| SHR 1 | 0 0 1 1 0 + 1 1 0 | |
| S = S + A | ||
| S | 1 1 1 1 0 |
В итоге получен тот же результат, что и перемножении вручную, то есть А*В = 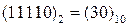 .
.
Сдвиг в компьютере суммы частичного произведения вправо, а не сдвиг множителя влево, как это делается при перемножении вручную, производится из соображений упрощения технической реализации. При этом, как видно из примера, результат остается неизменным.
Умножение чисел с различными знаками можно свести к перемножению их модулей с последующим формированием знакового разряда произведения. Произведению устанавливается знак плюс, если знаки чисел одинаковы и знак минус, если знаки чисел различны.
Кроме того, в компьютере есть возможность выполнять операции умножения чисел, представленных их кодами. При этом, положительные множители представляются в прямом коде, а отрицательные – в дополнительном. Если множители имеют одинаковые знаки, то произведение представляется в прямом коде, если же знаки различны, то произведение представляется в дополнительном коде.
Принципы реализации операции умножения чисел, представленных в форме с фиксированной точкой аналогичны, с той лишь разницей, что при этом добавляется операция определения порядка произведения (алгебраического сложения порядков сомножителей) и проводится, если необходимо, нормализация результирующей мантиссы с соответствующим изменением порядка произведения.
Если при суммировании порядков возникло переполнение, и порядок произведения получился отрицательным, то это означает, что искомое произведение оказалось меньше минимально представленного в компьютере числа, и тогда в качестве результата операции может быть записан нуль без перемножений мантисс множителей. Если же возникло переполнение для положительного порядка, то результат при этом может все-таки находиться в диапазоне чисел, представляемых в компьютере. Это объясняется тем, что при умножении мантисс происходит нарушение нормализации вправо, поэтому после нормализации мантиссы переполнение в порядке произведения исчезает
Операция деления чисел, представляемых в форме с фиксированной точкой, сводится к многократным вычитаниям и сдвигам. При этом разряды частного, начиная со старшего, определяются последовательным вычитанием делителя сначала из делимого, а затем из образующихся в процессе деления сдвигаемых остатков. Если разность между делимым (или очередным остатком) и делителем положительная или равна нулю, то в соответствующий разряд частного записывается единица, а если отрицательная – нуль. Поскольку в компьютере операция вычитания в непосредственном виде не выполняется, то последовательное вычитание заменяется сложением остатков с дополнительным кодом делителя. При этом новый остаток также получается в соответствующем коде.
В компьютере делимое в форме с фиксированной точкой представляется с удвоенным количеством разрядов по сравнению с делителем и частным.
6.4 Кодирование алфавитно – цифровой информации
Современные компьютеры обрабатывают не только цифровую, но и текстовую информацию. Проще говоря, алфавитно – цифровую информацию, содержащую цифры, буквы, знаки препинания, математические и другие символы.
В настоящее время широкое распространение получило кодирование символов с использованием однобайтовых ячеек памяти, которая может содержать 256 различных вариантов информации, отвечающей тому или иному символу. Это в полной мере перекрывает количество символов, содержащихся в алфавитах различных языков. Принцип кодирования символов состоит в том, что каждому символу в соответствии с принятой таблицей кодов ASCII соответствует определенное десятичное число. Затем это число переводится в двоичное. Например, выражение USSR 1917 будет храниться в памяти в восьми байтах
U S S R
01110010 11100010 11100010 11011001
1 9 1 7
11110001 11111001 11110001 11110111
а число –6.285 запишется в памяти в двоичном коде как
- 6. 2 8 5
01100000 11110110 01001011 11110010 11111000 11110101.
|
|
|
|
|
Дата добавления: 2014-01-14; Просмотров: 508; Нарушение авторских прав?; Мы поможем в написании вашей работы!