Тригонометрические ряды Фурье

В различных отраслях науки, в том числе, в физике приходится иметь дело с периодическими явлениями. Простейший пример – электрические колебания. Периодической называется функция 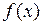, для которой существует такая величина 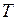, называемая периодом, что 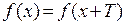. Простейшими 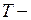периодическими функциями являются тригонометрические функции вида 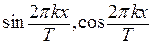, где 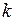– целое число, называемые гармониками. Представление периодической функции в виде суммы гармоник называется гармоническим анализом. В случае, когда такая сумма бесконечна, мы получаем тригонометрический ряд, называемый рядом Фурье.

Итак, пусть непрерывная 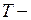периодическая функция 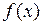представлена в виде тригонометрического ряда: 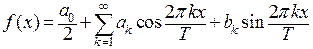. Возникает вопрос: как найти коэффициенты ?

Воспользуемся тем, что гармоники обладают следующим свойством:

,

,

,

,

,

,

.

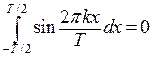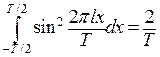Теперь для того, чтобы, например, найти 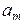умножим обе части равенства

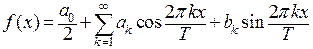на 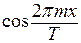и проинтегрируем на отрезке 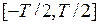. С учетом свойств гармоник в правой части равенства останется только слагаемое 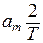, а в левой части – выражение 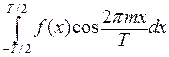. Отсюда мы получим .

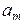Умножая на и интегрируя, получим .

А для того, чтобы получить 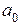, нужно просто проинтегрировать обе части равенства 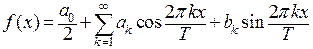на отрезке .

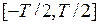Таким образом, непрерывная периодическая функция 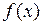представима в виде следующего тригонометрического ряда Фурье:

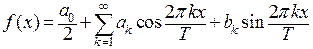, где ,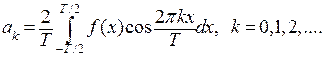

Заметим, что в случае, когда 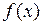четная на отрезке 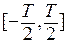, коэффициенты при синусах обратятся в ноль. Если 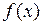нечетная на отрезке 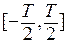, исчезнут коэффициенты при косинусах и свободный член.

В случае, когда периодическая функция имеет точки разрыва, ее также можно раскладывать в ряд Фурье, но равенство функции и суммы ряда будет только в точках непрерывности функции. В точках разрыва ряд Фурье будет сходиться к полусумме значений функции слева и справа от точки разрыва: .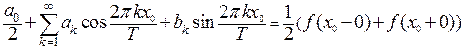

Возможно разложение функции в ряд Фурье с помощью MAXIMы. Мы получим все коэффициенты ряда Фурье для функции 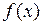, заданной на отрезке и -периодически продолженной на всю вещественную ось, если введем load(fourie); fourier (f(x),x,t) и нажмем Shift+Enter.

П р и м е р. Получим коэффициенты ряда Фурье для функции 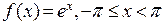. Для этого введем load(fourie); fourier(%e^x,x,%pi), нажмем Shift+Enterи получим

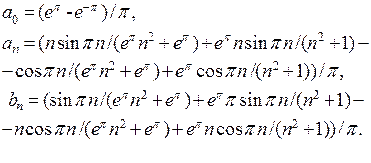
Мы видим, что коэффициенты содержат выражения 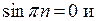. Поэтому преобразуем коэффициенты:

Для того, чтобы не только вычислить коэффициенты ряда Фурье, но и получить разложение функции 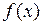, заданной на отрезке и –периодически продолженной на всю вещественную ось в ряд Фурье, следует

ввести load(fourie); totalfourier (f(x),x,T) и нажать Shift+Enter.

П р и м е р. Для разложения в ряд Фурье функции из предыдущего примера введем load(fourie); totalfourier (%e^x, x, %pi). При этом получим разложение

Следует отметить, что частные суммы ряда Фурье приближают исходную функцию не в конкретных точках, а «в среднем по отрезку». Сравним заданную функцию 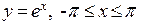, и 9-ю частную сумму ряда Фурье на одном графике. Для этого сначала введем функцию 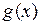, совпадающую с 9-й частной суммой, а затем нарисуем функцию (черным цветом) и функцию 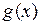(красным цветом) на одном графике над отрезком :

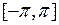g(x):=-(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1)*sum((n*(-1)^n*sin(n*x))/(n^2+1),n,1,9))/%pi+(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1)*sum(((-1)^n*cos(n*x))/(n^2+1),n,1,9))/%pi+

(%e^(-%pi)*(%e^%pi-1)*(%e^%pi+1))/(2*%pi);

load(draw); draw2d(explicit(%e^x,x,-%pi,%pi), color=red, explicit(g(x),x,-%pi,%pi)).

В результате получим картину

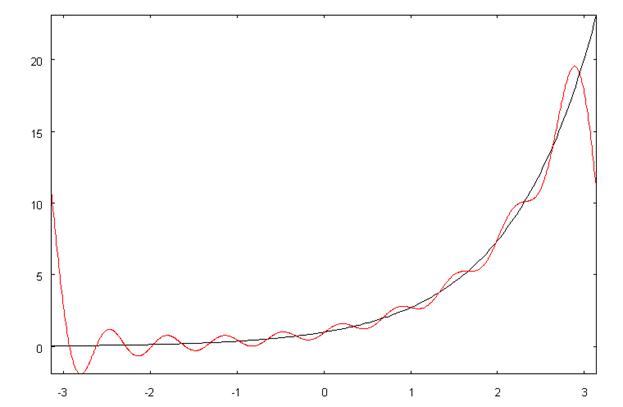
Здесь видно, что в конечных точках отрезка, где функция 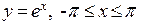, при периодическом продолжении с отрезка 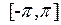в другие точки вещественной оси терпит разрыв, график частной суммы ряда Фурье (красная линия) значительно отличается от графика экспоненциальной функции. Если брать частную сумму с большим количеством членов, то график частной суммы будет теснее приближаться к исходной функции во внутренних точках интервала 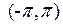, но вблизи точек поведение будет тем же из-за разрыва исходной функции при периодическом продолжении.

Мы видим, что если задать функцию на симметричном интервале 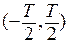, то ряд Фурье, построенный для этой функции, автоматически продолжает исходную функцию 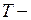периодически на всю вещественную ось. Оказывается, можно задать функцию на полуинтервале , продолжить ее четным или нечетным образом на симметричный полуинтервал 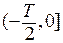и уже затем продолжить полученную на интервале 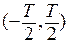четную или нечетную функцию 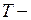периодически на всю вещественную ось. Для этого следует применить разложение в ряд Фурье по косинусам или по синусам, соответственно.

П р и м е р. Зададим на интервале функцию .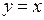

Разложим функцию в ряд по косинусам с помощью MAXIM-ы. Для этого применим команду load(fourie); fourcos (x, x, %pi). Мы получим коэффициенты 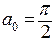и 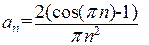. График частной суммы ряда на интервале 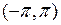до 10-го члена получим по команде plot2d(%pi/2+ sum((2*(cos(%pi*n)/n^2-1/n^2))/%pi*cos(n*x),n,1,10),[x,-%pi,%pi]).

Разложим функцию в ряд по синусам по команде load(fourie); foursin(x,x,%pi). Коэффициенты ряда имеют вид 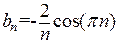. Очевидно, что частные суммы соответствующего ряда сходятся медленнее, чем частные суммы в предыдущем случае. График частной суммы ряда на интервале 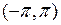до 20-го члена получим по команде plot2d(sum((2*(-cos(%pi*n)/n)) *sin(n*x),n,1,20),[x,-%pi,%pi]).

Дата добавления: 2014-01-14