Соотношение неопределенностей

В классической механике состояние материальной точки в каждый момент времени характеризуется ее положением и импульсом. Реальные микрочастицы-электроны, протоны, атомы и прочие - более сложные объекты. Нельзя характеризовать мгновенное состояние микрочастицы точными заданиями ее положения и импульса. Причина этого в том, что всякая микрочастица проявляет и корпускулярные и волновые свойства. Нельзя сказать, что в определенной точке пространства длина волны есть характеристика синусоиды, которая есть периодическая кривая.

С другой стороны, если какое-либо волновое образование занимает ограниченную область пространства, то его всегда можно представить синусоидами. Только одной синусоиды для этого недостаточно. Требуется волновой пакет - суперпозиция множества синусоид различных частот, которые усиливались бы в определенном интервале пространства ∆ х и взаимно гасили бы друг друга вне этого интервала. Если длина волнового пакета ∆ х, то волновые числа k, необходимые для его образования, не могут занимать как угодно узкий интервал. Минимальная ширина интервала должна удовлетворять условию:

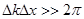. (4.3)

Это чисто волновое соотношение.

Выражая 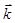через 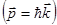, соотношение (4.3) можно переписать в виде:

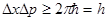. (4.4)

Это соотношение называется соотношением или принципомнеопределенности Гейзенберга для координаты и импульса частицы.

Чем точнее х, тем с меньшей точностью возможно характеризовать р, и наоборот. Но соотношение Гейзенберга никоим образом нельзя толковать в том смысле, что частица в каждый момент времени имеет определенные значения х и р, но мы их не можем узнать с большей точностью, чем это позволяет соотношение неопределенностей. Истинный смысл соотношения (4.4) отражает тот факт, что в природе объективно не существует состояния частиц с точно определенными значениями х и р.

Более точно соотношение неопределенностей записывается в виде:

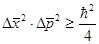(4.4 а)

- где 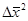, 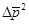- средние квадраты отклонения величин от среднего. , .

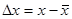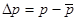Распространим соотношение неопределенностей на случай макроскопических тел. Возьмем маленький шарик m = 1 г. Определим положение этого шарика с точностью до размера атома ∆ х = 10^-10 м. Тогда неопределенность импульса будет 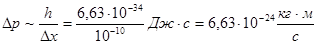, а неопределенность скорости импульса 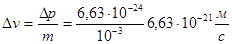. Такая точность недоступна никакому измерению.

Совсем иначе обстоит дело с движением электрона в атоме. Имеет ли смысл говорить о классическом движении электрона по боровской орбите?

Возьмем для определенности атом водорода и первую боровскую орбиту. Чтобы такое движение имело смысл, неопределенность ∆ r радиуса должна быть мала по сравнению с самим радиусом орбиты 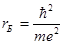. Но в этом случае неопределенность импульса будет

,

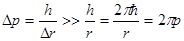что превосходит сам импульс электрона .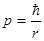

При таких условиях представление о движении по классическим орбитам теряет смысл. Поэтому квантовая механика при описании движений электронов в атомах отказалась от понятий траектории - этому понятию здесь реально ничего не соответствует.

Отметим некоторые выводы, вытекающие из соотношения неопределенностей (4.4):

1) состояние, в котором частица находится в полном покое,

2) невозможно;

2) в квантовой механике теряет смысл деление полной энергии Е на кинетическую и потенциальную. Действительно, одна из этих величин зависит от импульсов, другая - от координат. Эти же переменные не могут иметь одновременно определенные значения. Энергия Е должна определяться и измеряться лишь как полная.

Наряду с соотношением (4.4) в волновой теории выводится также соотно- шение

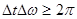. (4.5)

Смысл этого соотношения состоит в том, что ограниченный во времени волновой процесс не может быть монохроматическим. Если процесс длится в течение времени ∆ t, то разброс частот ∆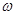, входящих в него волн удовлетворяет соотношению (4.5).

Если частоте ω сопоставить энергию 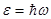, то формула (4.5) перейдет в выражение

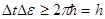. (4.6)

Формула (4.6) называется соотношением неопределенностей Гейзенберга для времени и энергии.

Соотношение (4.6) означает, что чем короче время существования какого-то состояния, тем с меньшей определенностью можно говорить об энергии этого состояния. И наоборот, чем больше это время, тем с большей точностью определена энергия состояния. Если состояние стационарно, то оно может существовать бесконечно долго. Именно по этой причине энергия стационарного состояния имеет вполне определенное значение.

Дата добавления: 2014-01-14