Элементы теории плоского векторного поля

Оповещение пользователя об ошибках ввода

Проверка на уровне формы

Она позволяет проверить одновременно все поля формы. Например, в двух текстовых полях задаются границы интервала, каждая из них может быть нормальным числом, не выходящим за допустимые пределы, но при этом как границы они будут неверны.

Для запуска проверки обычно используется событие Closing формы или событие нажатия кнопки (OK, Применить и т.д.). В обработчик события Closing также передается объект класса CancelEventArgs.

Делать это можно по разному:

- с помощью модельного окна с сообщением MessageBox.Show ("Ошибка ввода");

- с помощью изменения цвета текста или фона текстового поля с неверно введенными данными;

- с помощью компонента ErrorProvider

Компонент позволяет задать для каждого элемента управления текст сообщения об ошибке, если этот текст задан, то рядом с элементом управления появляется мигающий значок (его вид можно задать в свойствах компонента). А при наведение указателя мыши на значок появляется текст сообщения об ошибке.

if(notEmptyTextBox.Text.Equals(""))

myErrorProvider.SetError(notEmptyTextBox, "Поле не может быть пустым");

else

myErrorProvider.SetError(notEmptyTextBox, "");

В качестве иллюстрации теории плоского векторного поля будем применять поле скоростей плоско-параллельного течения жидкости. Пусть 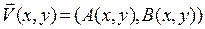– вектор скорости в точке с координатами 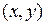. Представим, что поле течения жидкости потенциально и соленоидально, что соответствует течению идеальной жидкости. Потенциальность означает выполнение равенства 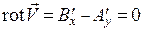. Соленоидальность означает выполнение равенства .

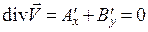Введем две функции переменных 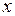и 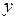: 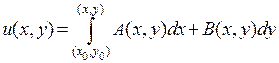, 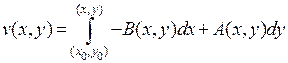. Вследствие произвольности точки 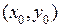каждая из введенных функций 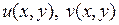определяется с точностью до произвольного вещественного слагаемого. Пути интегрирования во введенных интегралах не указаны, так как согласно условиями потенциальности и соленоидальности эти интегралы не зависят от пути интегрирования. Мы видим, что введенные функции удовлетворяют равенствам , и значит, являются комплексно-сопряженными функциями. Следовательно, 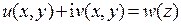– аналитическая функция комплексного переменного 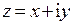. Эту функцию, заданную в области определения поля скоростей, называют комплексным потенциалом поля скоростей. Заметим, что

,

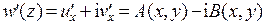и значит, по комплексному потенциалу легко определить скорость в соответствующей точке: .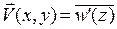

Линией тока называется та линия в области течения жидкости, касательная к которой в каждой точке параллельна вектору скорости в соответствующей точке. Таким образом, линии тока – это линии, вдоль которых перемещается жидкость. В соответствии с определением дифференциальное уравнение линий тока имеет вид: или 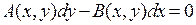. Это значит, что вдоль линий тока имеем 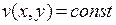. Если теперь представить конформное отображение области течения жидкости, полученное применением аналитической функцией 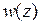, то линии тока в плоскости течения перейдут в горизонтальные линии в плоскости комплексного потенциала.

Это свойство позволяет находить скорости в произвольных точках области течения в результате применения конформного отображения области течения на область с горизонтальными границами. Приведем примеры применения таких конформных отображений.

1. Задача обтекания бесконечной кривой. Следует найти скорости в любой точке бесконечной области течения, ограниченной бесконечной кривой 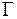, если известно значение скорости в бесконечно удаленной точке.

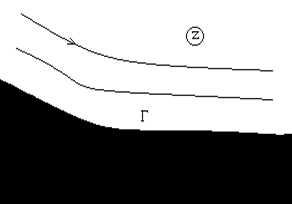
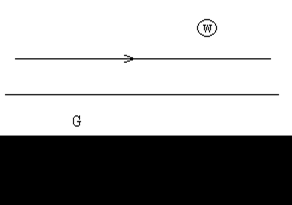
Для решения задачи следует конформно отобразить бесконечную область течения в плоскости z на полуплоскость в плоскости w так, чтобы граница Г (линия тока) перешла в горизонтальную прямую G – границу полуплоскости. При этом необходимо, чтобы бесконечно удаленная точка в плоскости z перешла в бесконечную точку в плоскости w. Кроме того, отображающая функция 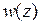должна обладать следующим свойством: .

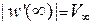П р и м е р. Исследовать обтекание бесконечной прямой с выпуклостью в виде границы полукруга радиуса R. Вектор скорости в бесконечности имеет величину .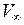

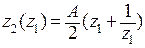Пусть граница области течения лежит на оси OX, центр круга, половина которого является выпуклостью на прямой, находится в начале координат. Функция отображает область течения на подобную область, где выпуклость имеет радиус 1. Теперь функция при 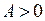отображает область в плоскости 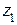на верхнюю полуплоскость, причем бесконечность переходит бесконечность. Следовательно, . Остается подобрать число A так, чтобы скорость в бесконечности была заданной. Так как 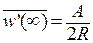, получим комплексный потенциал: .

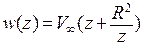Предположим, что нужно узнать скорость потока в точке 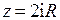. Для этого найдем .

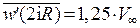2. Течение жидкости в канале. Следует найти скорости в любой точке бесконечной области течения, ограниченной двумя бесконечными кривыми, если известно значение расхода жидкости .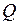

Расходом жидкости в канале называют количество жидкости, протекающее за единицу времени перпендикулярно любой кривой, соединяющей берега канала, то есть, ,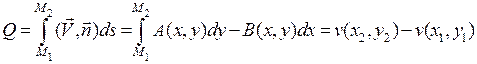

где 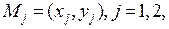– точки на разных берегах канала. Поскольку комплексный потенциал отображает берега канала на горизонтальные прямые в плоскости 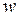, значение 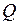совпадает с шириной полосы в плоскости комплексного потенциала. Поэтому для решения поставленной задачи следует отобразить криволинейную полосу, изображающую канал, на горизонтальную полосу шириной 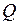с соответствием .

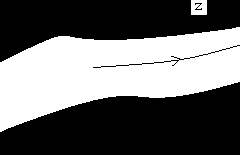
П р и м е р. Исследовать течение жидкости в бесконечном канале с перпендикулярным штифтом, торчащим из одной из стенок канала.

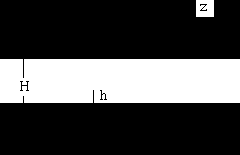
Пусть ширина канала равна H, высота штифта равна h, причем 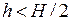. Пусть сторона с штифтом расположена на оси OX, причем основание штифта в начале координат.

Преобразование 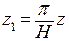переводит область течения в подобную полосу с надрезом ширины 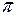, причем высота надреза равна 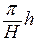. Функция 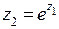переводит область в плоскости 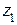на верхнюю полуплоскость с разрезом по дуге окружности радиуса 1 с центром в нуле от точки 1 до точки 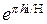. Теперь функция 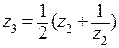отображает полученную в плоскости 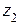область на плоскость с разрезом, лежащим на оси OX и соединяющим через бесконечность точки 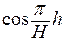и -1. Функция переводит область в плоскости 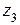на плоскость с разрезом вдоль положительной части оси OX, при этом образом бесконечно удаленной точки является 1. Функция при соответствующем выборе ветви переводит область в плоскости 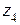на верхнюю полуплоскость. Теперь верхнюю полуплоскость переведем в себя так, чтобы точка 1 перешла в бесконечно удаленную точку, а точка -1 в ноль. Это сделает функция 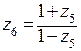. И наконец, полуплоскость переведем в полосу шириной 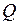с помощью функции 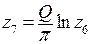. В итоге комплексным потенциалом будет суперпозиция всех перечисленных функций: 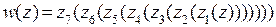. То есть, .

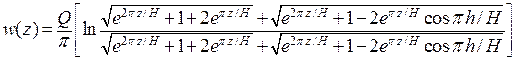Теперь, чтобы получить значение скорости в любой точке области течения, следует взять комплексное сопряжение от производной 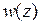в соответствующей точке.

Дата добавления: 2014-01-14