Вывод бигармонического оператора

Для решения плоской задачи теории упругости методом конечных разностей плоское тело покрывается сеткой и разыскивается функция напряжений только в узлах сетки (Рис. 10). Значение функции напряжений в узлах обозначаем индексом. Например, является значением функции напряжений в узле сетки по пересечению линий (m, n). В каждом узле сетки дифференциальные соотношения заменяются конечно – разностными. Первая производная по x функции напряжений в узле пересечения линий (m, n) представляется выражением (4-а), т.е.

(5)

Используя выражение (4), записываем вторую частную производную

(6)

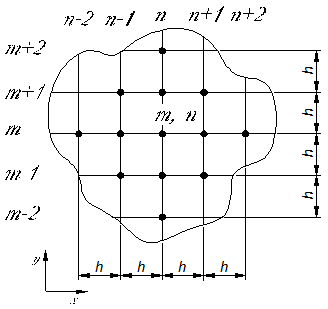
Рисунок10.

Узлы сетки, входящие в уравнение для точки

или в форме оператора

(6-а)

Вторая частная производная по y может быть вычислена аналогично

(7)

чи у вигляді оператора

(7-а)

Гармонический оператор при квадратной сетке имеет вид

(8)

или для произвольной точки

(8-а)

Для получения бигармонического оператора уравнение (1) изображается в виде

,

т.е.

,

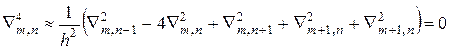или, используя оператор (8-а) для каждой точки, входящей в эту зависимость, получаем

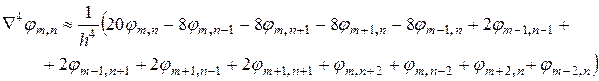(10)

или для произвольной точки

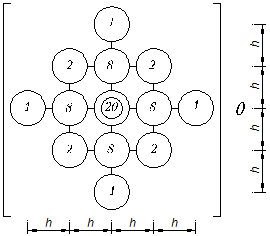
(9-а)

Таким образом, дифференциальное уравнение в каждой точке (m, n) можно заменить разностными уравнениями, то есть уравнениями для конечного числа приближенных значений . Для каждой точки деления (m, n) (m =1,2,3,…, M; n= 1,2,3,… ,N) составляются разностные уравнения, которые составляют систему линейных алгебраических уравнений относительно значений функции напряжений во всех внутренних узлах сетки 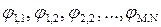, которые называются основными неизвестными метода конечных разностей (метода сеток). После решения системы относительно значений функции напряжений можно, используявыражения (6) и (7), получить нормальные напряжения 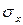и в каждой точке. Для вычисления касательных напряжений необходимо конечно – разностное соотношение для вычисления второй смешанной производной

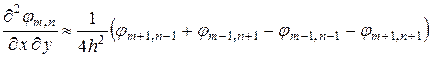(10)

Касательное напряжение в точке 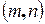вычисляется следующим образом

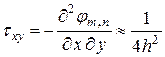
(11)

Более точные значения можно получить в цетре квадрата меду узлами сетки, они вычисляются следующим образом

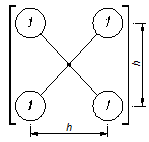
			(12)

При составлении уравнений для точек, отстоящих на шаг сетки от контура упругого тела, бигармонический оператор захватывает точки законтурные. Значения функции напряжений в этих точках определяют из условия равенства нормальной производной продольной силе, т.е.

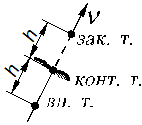
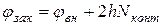
Дата добавления: 2014-01-14