Представление гармонических колебаний

Электрические цепи могут находиться под воздействием постоянных или переменных напряжений и токов. Среди этих воздействий важнейшую роль играют гармонические колебания. Последние широко используются для передачи сигналов и электрической энергии, а также могут применяться в качестве простейшего испытательного сигнала. Исследование режима гармонических колебаний важно и с методической точки зрения, поскольку анализ электрических цепей при негармонических воздействиях можно свести к анализу цепи от совокупности гармонических воздействий. В этом смысле методику анализа и расчета цепей при гармонических воздействиях можно распространить и на цепи при периодических несинусоидальных, а также непериодических воздействиях.

Гармоническое колебание i(t) (рисунок 5.1) характеризуется следующими основными параметрами: амплитудой I_m, угловой частотой w, начальной фазой j₀.Начальная фаза j₀ = wt₀ так как j = wt (или t = j/w).

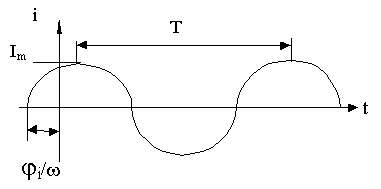
Рисунок 5.1 - Гармонический сигнал

Аналитически гармонические колебания можно определить уравнением:

i(t) = I_msin(w t + j₀). (1)

Для питания различных электроэнергетических установок в СССР принята промышленная частота f = 50 Гц. В качестве источников гармонических колебаний промышленной частоты используются электромашинные генераторы различного типа. Электромашинные генераторы используются для получения гармонических напряжений и токов не выше 5-8 кГц. Для получения гармонических сигналов более высоких частот обычно используются ламповые и полупроводниковые генераторы.

Важными параметрами гармонических колебаний являются их действующее и среднее значения. Действующее значение гармонического тока:

. (2)

После интегрирования получим для действующего значения тока:

. (3)

Аналогично определяется действующее значение напряжения: U» 0,707U_m. Действующие значения токов и напряжений называют еще их
среднеквадратичными значениями.

Среднее значение гармонического тока:

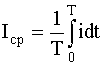. (4)

Для гармонического тока I_ср = 0. Этот результат понятен, если учесть, что уравнение определяет площадь, ограниченную кривой i(t) за период Т.

Гармонические колебания можно представить различными способами: функциями времени (временные диаграммы); вращающимися векторами (векторные диаграммы); комплексными числами; амплитудными и фазовыми спектрами. Тот или иной способ представления применяется в зависимости от характера решаемых задач.

1) Временное представление гармонических колебаний наглядно, однако его использование в задачах анализа цепей затруднительно, так как требует проведения громоздких тригонометрических преобразований (иллюстрация).

2) Более удобно векторное представление гармонических колебаний, при котором каждому колебанию ставится в соответствие вращающийся вектор определенной длины с заданной начальной фазой. На рисунке 5.2а показано векторное представление двух колебаний i₁ и i₂: i₁ = I_m1sin(wt + j₁); i₂ = I_m2sin(wt + j₂).

Их сумму i₃ можно найти по формулам суммирования векторов:

i₃ = i₁ + i₂ = I_m3sin(wt + j₃), (5)

где ;

.

Рисунок 5.2 - Представление гармонических колебаний

Величина j = j₂ - j₁ называется фазовым сдвигом между колебаниями i₁ и i₂.

Совокупность векторов, изображающих гармонические колебания в электрической цепи, называют векторной диаграммой. Векторные диаграммы можно строить как для амплитудных, так и для действующих значений токов и напряжений.

3) Наиболее распространенными являются представления гармонических колебаний с помощью комплексных чисел. Эти представления лежат в основе символического метода расчета электрических цепей - метода комплексных амплитуд. Представим ток i на комплексной плоскости. Для этого изобразим вектор I_m на комплексной плоскости с учетом начальной фазы j (рисунок 5.2б). Будем вращать этот вектор в положительном направлении (против часовой стрелки) с угловой частотой w. Тогда в любой момент времени положение вращающегося вектора определится комплексной величиной (комплексным гармоническим колебанием) (иллюстрация):

i(t) = I_me^{j(w t + j)} = I_mcos(wt + j_i) + jI_msin(wt + j_i). (6)

Первая часть слагаемого отражает проекцию вращающегося вектора на вещественную ось, а вторая часть - на мнимую ось. Оценив второе слагаемое, приходим к выводу: синусоидальный ток i на комплексной плоскости представляется в форме проекции на мнимую ось вращающегося вектора:

i = Im[I_me^{j(w t + j)}] = Im [_me^jwt], (7)

где Im - сокращенное обозначение слова Imaginarins (мнимый);

.

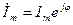Величина 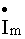носит название комплексной амплитуды тока.

Если гармоническое колебание задается в форме косинусоиды, то на комплексной плоскости этому току соответствует проекция вектора на вещественную ось:

i = Re [I_me^{j(w t + j)}] = Re [_me^jwt], (8)

где Re - сокращенное обозначение слова Realis (действительный, вещественный).

Комплексную амплитуду синусоидальной функции заданной частоты можно рассматривать как преобразование временной функции в частотную область.

4) Спектральное (частотное) представление гармонических колебаний состоит в задании амплитудного и фазового спектров колебания (иллюстрация).

Гармонические колебания в пассивных R, L, C - цепях

Дата добавления: 2014-01-14