Простейший измерительный инструмент

ИЗМЕРИТЕЛЬНЫЙ ИНСТРУМЕНТ И ПРИЕМЫ ИЗМЕРЕНИЯ ДЕТАЛЕЙ

Самые простые измерительные инструменты — масштабные линейки и рулетки (рис. 9.4). На линейке и рулетке нанесены штрихи — деления, расположенные друг от друга на расстоянии 1 мм, реже — 0,5 мм. Эти деления и составляют измерительную шкалу.

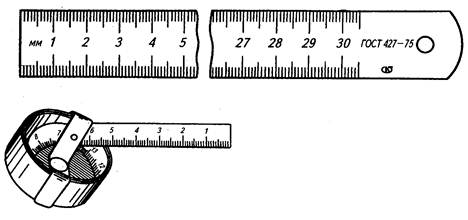
Рис. 9.4.

Масштабная линейка и рулетка

При измерении масштабную линейку прикладывают к изделию так, чтобы ее торец (нулевое деление) совпал с началом изделия, тогда деление, совпадающее с его концом, покажет размер изделия в мм (рис. 9.5) При этом необходимо располагать линейку вдоль стороны или оси изделия, не допуская перекоса, в противном случае измерение будет неточным — размер, отсчитанный по шкале, будет больше действительного.

С помощью рулетки определяют, например, длину развертки или диаметр: большого цилиндра.

Масштабная линейка позволяет производить измерение с точностью до 0,5 мм, а рулетка — до 1 мм.

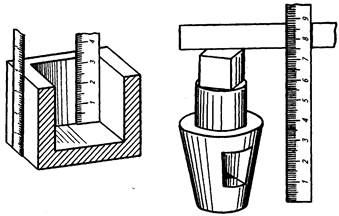
Рис. 9.5.

Примеры обмера деталей масштабной линейкой

Кронциркуль и нутромер служат соответственно для определения наружных и внутренних размеров изделий (рис. 9.6). Криволинейная форма ножек этих инструментов позволяет довольно точно производить измерения, а затем переносить замеренную величину на масштабную линейку.

Рис. 9.6.

Примеры обмера деталей кронциркулем и нутромером

Пользуясь этими инструментами, можно замерить не только элементы деталей типа «вал-отверстие», но и производить более сложные измерения.

К примеру, на рис. 9.7 показано определение диаметра D окружности расположения центров отверстий на круглом фланце. В одном случае, при определении величины диаметра кронциркулем, его ножки, упираясь в стенки отверстия, замеряют величину l. В этом случае D = l+ d, где d — диаметр отверстия. В другом — при замере нутромером, определяют величину L. В этом случае D = L — d.

Рис. 9.7.

Определение диаметра межцентрового расстояния с помощью кронциркуля и нутромера

С помощью кронциркуля возможно определить толщину стенки пустотелой детали (рис. 9.8) в труднодоступном для измерения месте. Если толщину стенки детали непосредственно замерить невозможно, так как нельзя извлечь кронциркуль, не раздвигая его ножек, то измерение производят следующим образом. В замеряемом месте к стенке детали прикладывают торцом линейку. Ножки кронциркуля раздвигают на произвольную величину, например, на размер С. Затем заводят одну ножку внутрь детали до упора в стенку изнутри детали, а другую прикладывают к линейке и определяют величину В. Теперь кронциркуль можно вынуть и приложить к линейке. Толщина стенки детали А = С - В.

Для успешного пользования кронциркулем и нутромером требуется навык. Точность измерения этими инструментами при определенном опыте может быть достигнута 0,5 мм.

Косвенные методы измерения. К косвенным методам измерения приходится прибегать зачастую в различных случаях, когда по каким-либо причинам нет возможности произвести прямые измерения прикладыванием инструмента к изделию.

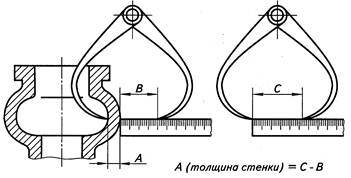
Рис. 9.8.

Определение толщины стенки детали с помощью кронциркуля в труднодоступном месте

На рис. 9.9 показано определение диаметра большого вала по хорде и высоте сегмента с помощью штангенциркуля. В этом случае диаметр вала определяют по формуле:

D =l²/(4h)+h

где l — хорда, а h — высота сегмента.

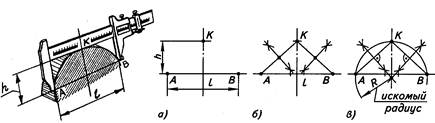
Рис. 9.9.

Определение величины диаметра вала по хорде

Диаметр вала можно определить менее точно и графическим построением. Для этого по трем точкам (А, В и К), вычерченным на листе бумаги с установленными между ними расстояниями, определяем вначале центр (О) описанной окружности. Теперь можно построить радиус описанной окружности и замерить его линейкой. Разумеется, в этом случае все построения необходимо производить как можно с большей достижимой точностью.

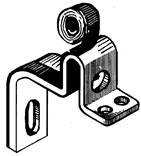
Рис. 9.10.

Определение длины развертки сложно изогнутой детали

Измерить изогнутую деталь сложной формы (рис. 9.10), например, для определения величины заготовки для развертки, обычной линейкой или рулеткой невозможно, так как не представляется возможным обеспечить полное прилегание мерительного полотна к детали по всей ее длине. Обойти это затруднение можно, воспользовавшись куском изоляционной ленты, определить длину которой уже не составит труда.

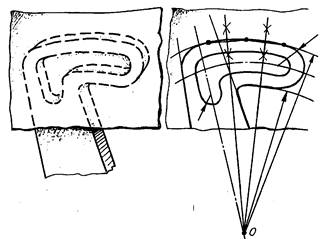
Рис. 9.11.

Обмер детали криволинейной формы способом «обжима»

В тех случаях, когда приходится иметь дело с деталями, имеющими криволинейные очертания, удобнее всего положить изделие на бумагу и обвести контур карандашом. Если же это по каким-либо причинам невозможно сделать, то поступают следующим образом. Наложив на интересующую нас часть изделия лист тонкой бумаги, обминают ее по контуру с целью получения отпечатка. Затем полученный контур обводят карандашом (рис.9.11). Теперь уже на бумаге можно выполнить дополнительные построения, с помощью которых возможно определить часть размеров, остальные определяются замером с натуры.

Для измерения и определения радиусов округления большой величины, можно использовать и такой способ. В картонку, вырезанную в виде пластинки, вставлены, как указано на рис. 9.12, булавки или тонкие металлические стерженьки. Все это устройство располагают над кривой поверхностью так, чтобы все булавки или стерженьки касались ее. Теперь осталось зафиксировать на бумаге установленные точки и вышеуказанным способом определить искомый радиус скругленной поверхности.

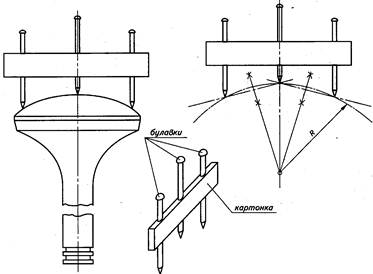
Рис. 9.12.

Определение величины радиуса дуги

Дата добавления: 2014-01-14